Pitman estimator

An equivariant estimator for the shift parameter with respect to a group of real shifts, having minimal risk with respect to a quadratic loss function.

Let the components 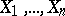of a random vector be independent random variables having the same probability law, with probability density belonging to the family

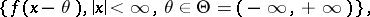and with

for any 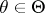. Also, let 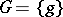be the group of real shifts operating in the realization space of :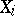

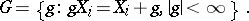In this case, the task of estimating 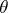is invariant with respect to the quadratic loss function 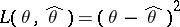if one uses an equivariant estimator 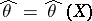of 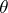, i.e. 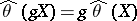for all 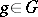. E. Pitman [1] has shown that the equivariant estimator 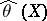for the shift parameter with respect to the group 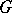that has minimal risk with respect to the quadratic loss function takes the form

where 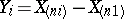, and 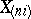is the 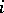-th order statistic of the observation vector 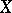. The Pitman estimator is unbiased (cf. Unbiased estimator); it is a minimax estimator in the class of all estimators for 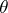with respect to the quadratic loss function if all equivariant estimators for 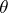have finite risk function [2].

Example 1. If

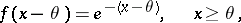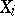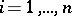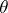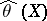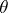i.e. , , has exponential distribution with unknown shift parameter , then the Pitman estimator for is

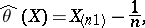and its variance is .

Example 2. If

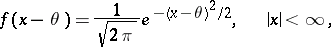i.e. 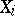, , 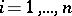has normal distribution 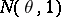with unknown mathematical expectation 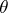, then the arithmetic mean

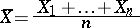is the Pitman estimator.

References

[1]	E.J. Pitman, "The estimation of the location and scale parameters of a continuous population of any given form" Biometrika , 30 (1939) pp. 391–421
[2]	M.A. Girshick, L.J. Savage, "Bayes and minimax estimates for quadratic loss functions" J. Neyman (ed.) , Proc. 2-nd Berkeley Symp. Math. Statist. Prob. , Univ. California Press (1951) pp. 53–73
[3]	S. Zachs, "The theory of statistical inference" , Wiley (1971)