Small category

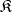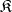A category whose class of morphisms is a set. A small category is called a 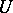-category if 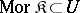, where 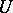is a universe. For a small category and an arbitrary locally small category 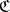the category of covariant (contravariant) functors (cf. Functor) from 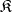to 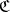is locally small. In particular, the small categories form the closed category 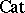of small categories, one of the basic categories of mathematics [1].

References

[1]	F.W. Lawvere, "The category of categories as a foundation for mathematics" S. Eilenberg (ed.) et al. (ed.) , Proc. conf. categorical algebra (La Jolla, 1965) , Springer (1966) pp. 1–20

Comments

A category is called locally small if, for any pair of objects 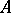and 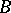, the class of morphisms from 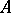to 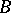is a set. (Some authors assume this condition as part of the definition of a category.) A locally small category is small if and only if its class of objects is a set.

Cf. also Universe.