Information, amount of
An information-theoretical measure of the quantity of information contained in one random variable relative to another random variable. Let 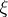 and
and 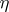 be random variables defined on a probability space
be random variables defined on a probability space 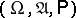 and taking values in measurable spaces (cf. Measurable space)
and taking values in measurable spaces (cf. Measurable space) 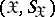 and
and 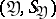 , respectively. Let
, respectively. Let 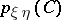 ,
, 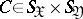 , and
, and 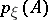 ,
, 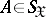 ,
, 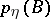 ,
, 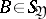 , be their joint and marginale probability distributions. If
, be their joint and marginale probability distributions. If 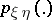 is absolutely continuous with respect to the direct product of measures
is absolutely continuous with respect to the direct product of measures 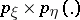 , if
, if 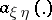 is the (Radon–Nikodým) density of
is the (Radon–Nikodým) density of 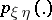 with respect to
with respect to 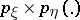 , and if
, and if 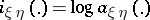 is the information density (the logarithms are usually taken to base 2 or
is the information density (the logarithms are usually taken to base 2 or  ), then, by definition, the amount of information is given by
), then, by definition, the amount of information is given by
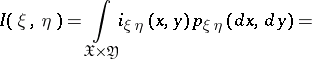 |
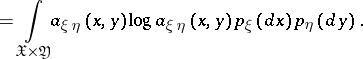 |
If 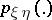 is not absolutely continuous with respect to
is not absolutely continuous with respect to 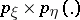 , then
, then 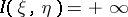 , by definition.
, by definition.
In case the random variables 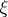 and
and 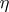 take only a finite number of values, the expression for
take only a finite number of values, the expression for 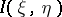 takes the form
takes the form
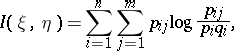 |
where
 |
are the probability functions of 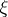 ,
, 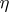 and the pair
and the pair 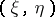 , respectively. (In particular,
, respectively. (In particular,
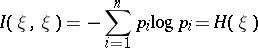 |
is the entropy of 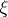 .) In case
.) In case 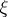 and
and 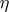 are random vectors and the densities
are random vectors and the densities 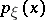 ,
, 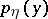 and
and 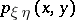 of
of 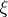 ,
, 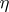 and the pair
and the pair 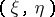 , respectively, exist, one has
, respectively, exist, one has
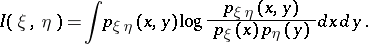 |
In general,
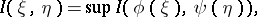 |
where the supremum is over all measurable functions 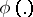 and
and 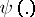 with a finite number of values. The concept of the amount of information is mainly used in the theory of information transmission.
with a finite number of values. The concept of the amount of information is mainly used in the theory of information transmission.
For references, see , ,
Information, amount of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Information,_amount_of&oldid=12464