Constructive quantum field theory

A branch of mathematical physics studying the properties of models of quantum field theory. One of the problems of constructive quantum field theory consists in the investigation of interacting quantum fields in real four-dimensional space-time. Mathematically, the existence of these fields has not yet been established (1987). Therefore the main efforts have been directed towards the study of the less singular models of quantum field theory in two- and three-dimensional space-time. Constructive quantum field theory is a synthesis of ideas and methods of axiomatic field theory and renormalization theory with modern mathematical methods. The concept of a relativistic quantum field itself admits various equivalent mathematical interpretations, enabling one to use methods from different areas of mathematics.

A quantum field can be treated either in terms of the theory of non-linear hyperbolic equations for operator-valued generalized functions, or in terms of the theory of generalized random fields (establishing a closed contact with statistical mechanics), or as a system of analytic functions of several complex variables (in the study of analytic properties of the 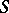-matrix), or it can be considered from the point of view of 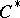-algebras and representation theory.

In the first works on constructive quantum field theory, mainly methods from functional analysis were used. A relativistic quantum field in two-dimensional space-time satisfying the Wightman axioms was first successfully constructed [8] using the Euclidean formulation [9] of quantum field theory, enabling one to invoke methods from probability theory and statistical mechanics.

A relativistic quantum field is completely characterized by its Wightman functions 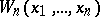. The equivalent Euclidean formulation of quantum field theory is given in terms of Schwinger functions 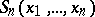(these are obtained from 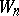by analytic continuation to the Euclidean points 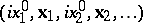), satisfying the Osterwalder–Schrader axioms. Under certain additional hypotheses it can be proved that the 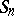are moments of a probability measure with special properties. The method of constructing models of quantum field theory in which one begins by constructing a probability measure and then verifies the Osterwalder–Schrader axioms for its moments has been proved most convenient and is most widespread.

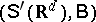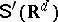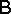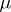In the simplest case of a single scalar field one considers a measurable space , where is the space of (real-valued) tempered distributions, and is the -algebra generated by the cylinder sets, and a class of probability measures on 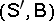possessing the following special properties.

1) On 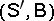there is defined a natural representation of the connected component 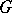of the identity of the Euclidean group of motions of 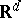by automorphisms of the 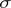-algebra 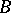. It is required that the measur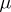e be -invariant. This condition is the Euclidean expression of relativistic invariance.

2) Let be the generalized random field on 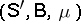defined by 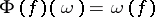, , 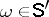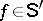. For any functi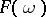on on 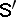one defines 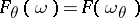, where , 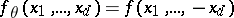. Let be the -algebra generated by the functions 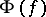with 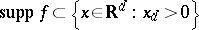. It is required that the positivity condition of Osterwalder–Schrader holds:

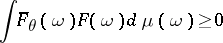for any 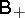-measurable 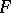on . This condition expresses the positive definiteness of the scalar product in relativistic Hilbert space. For two-dimensional models the somewhat stronger Markov condition for the field 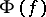is widely used.

3) It is required that there exists a norm on 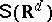such that

is uniformly bounded and continuous with respect to on

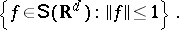4) The subgroup of translations of the group 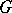must act ergodically. This expresses the uniqueness of vacuum in relativistic theory.

If the measure 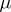satisfies the conditions 1)–4), then it is called a quantum measure, and the corresponding generalized random field 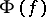is called a Euclidean field. The moments of the quantum measure,

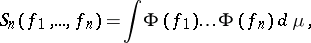are the Schwinger functions, which satisfy the Osterwalder–Schrader axioms. There exists a unique relativistic quantum field satisfying all Wightman axioms and such the analytic continuations of its Wightman functions to the Euclidean points are the same as the Schwinger functions of the given quantum measure 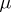. If a measure 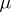satisfies conditions 1)–3) only, then conditions 1)–4) hold for all its ergodic components.

One class of quantum measures is easily constructed, namely the Gaussian measures (depending on a parameter 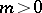) with characteristic functional

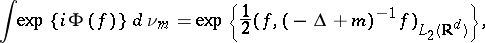where 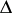is the Laplace operator. The corresponding Euclidean field is called the free (scalar) Euclidean field of mass .

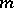The construction of non-Gaussian measures presents great difficulties, and the results depend essentially on the dimension 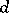. The usual procedure is as follows. A function 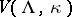is constructed on 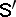(the interaction potential), depending on the parameters , called the volume cut-off, and 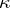, called the ultraviolet cut-off. Heuristically 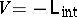(see Quantum field theory). 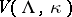is additive in 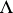, but not in 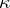. The measure

is then constructed (the definition of 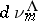is given below) and one studies the limits of the sequence of measure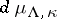s as 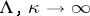. For certain potentials 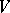, the limit measure 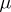satisfies conditions 1)–4). Convergence of the measures is usually understood in the sense of convergence of all moments and characteristic functionals.

For example, for models with interaction 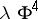with 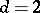, this procedure is made concrete in the following way. Let 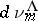be a Gaussian measure on 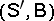with characteristic functional

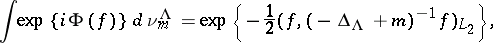where is a self-adjoint extension of the Laplace operator with certain boundary conditions on the boundary of the domain 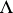in the plane 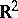(usually 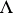is a rectangle); the kernel 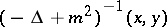can, for example, be the Green function for the Dirichlet problem. Suppose further that 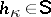and as 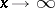. The random variable 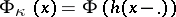is, for 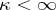, a smooth function of the parameter 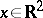and

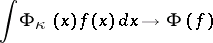as 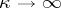. Set

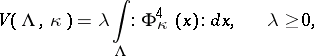where 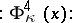is a Wick power of 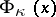(see Fock space). Then

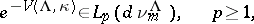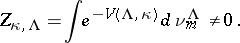Finally, let

As 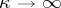, , 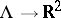all moments and characteristic functionals of the measures 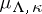converge to the moments and characteristic functionals of a certain quantum measure 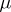. It turns out that for sufficiently large the measures 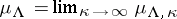with different boundary conditions on 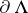have, in general, different limits as 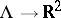. In this case it is said that there is a phase transition.

The central problem of constructive quantum field theory consists of describing all the quantum measures (phases) corresponding to a given interaction potential, and in studying the properties of the corresponding relativistic quantum fields. In the first instance one is interested in the spectral properties of the mass operator of the Poincaré group (the study of which reduces to examining the behaviour of the Schwinger functions at large distances) and the properties of the 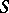-matrix such as its analyticity, unitarity, etc. (the 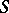-matrix is studied by analytic continuation of the Schwinger functions).

The existence of quantum measures for 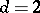was proved (1978) for interaction potentials 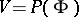, where 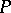is any polynomial that is bounded from below, 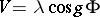(the sine-Gordon equation) and certain other non-polynomial interactions, as well as for some multi-components fields . For a sufficiently weak polynomial interaction a study has been undertaken of the dependence of the spectrum of the mass operator on the form of the polynomial, and the existence of the -matrix has been established. Fermion and scalar fields with Yukawa interaction have also been investigated. The Euclidean fermion field is not a generalized random field and takes values in a Grassmann algebra. However, one can "integrate out" the fermion variables and the problem then reduces to estimating certain path integrals with respect to ordinary Gaussian measures. All these models have phase transitions for certain values of the parameters.

The constructions of relativistic quantum fields described above lead only to the so-called vacuum sectors, that is, to quantum fields satisfying the Wightman axioms, supplemented by the axiom of existence of vacuum. These fields are solutions of non-linear equations with obvious initial conditions. For a number of two-dimensional models (sine-Gordon, etc.) soliton sectors have been constructed in which vacuum is absent but which have a discrete spectrum for the mass operator; from the physical point of view this is of great interest. These new sectors are constructed by means of special automorphisms of the 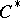-algebra of observables in the vacuum sector.

For 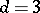, the existence has been proved of quantum measures in a model with 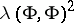interaction, where

Here the interaction potential has the form

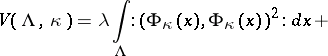where 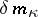and 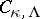are certain definite functions of 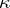and 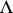; that is, counter terms are added. Also, in this model a phase transition occurs for sufficiently large 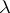, and it is accompanied by 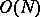-symmetry breakdown.

References

[1]	N.N. Bogolyubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian)
[2]	, Constructive quantum field theory , Lect. notes in physics , 25 , Springer (1973)
[3]	M. Reed, B. Simon, "Methods of modern mathematical physics" , 1–4 , Acad. Press (1972–1978)
[4]	B. Simon, "The 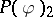model of Euclidean (quantum) field theory" , Princeton Univ. Press (1974)
[5]	C. Hepp, "Théorie de la renormalisation" , Lect. notes in physics , 2 , Springer (1969)
[6]	, Euclidean quantum field theory. The Markov approach , Moscow (1978) (In Russian; translated from English)
[7]	R.L. Dobrushin, R.A. Minlos, "Polynomials of linear random functions" Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 67–122 (In Russian)
[8]	J. Glimm, A. Jaffe, T. Spencer, "The Wightman axioms and particle structure in the 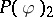quantum field model" Ann. of Math. , 100 : 3 (1974) pp. 585–632
[9]	E. Nelson, "Construction of quantum fields from Markoff fields" J. Funct. Anal. , 12 : 1 (1973) pp. 97–112
[10]	J. Fröhlich, "Schwinger functions and their generating functionals II. Markovian and generalized path space measures on 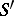" Adv. Math. , 23 : 2 (1977) pp. 119–181

References

[a1]	J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981)