Norm-residue symbol
norm residue, Hilbert symbol
A function that associates with an ordered pair of elements 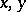 of the multiplicative group
of the multiplicative group 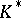 of a local field
of a local field 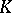 an element
an element 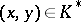 that is an
that is an  -th root of unity. This function can be defined as follows. Let
-th root of unity. This function can be defined as follows. Let 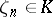 be a primitive
be a primitive  -th root of unity. The maximal Abelian extension
-th root of unity. The maximal Abelian extension 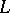 of
of 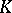 with Galois group
with Galois group  of exponent
of exponent  is obtained by adjoining to
is obtained by adjoining to 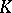 the roots
the roots 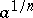 for all
for all  . On the other hand, there is a canonical isomorphism (the fundamental isomorphism of local class field theory)
. On the other hand, there is a canonical isomorphism (the fundamental isomorphism of local class field theory)
 |
The norm residue of the pair 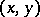 is defined by
is defined by
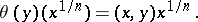 |
D. Hilbert introduced the concept of a norm-residue symbol in the special case of quadratic fields with 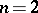 . In [4] there is an explicit definition of the norm residue using only local class field theory.
. In [4] there is an explicit definition of the norm residue using only local class field theory.
Properties of the symbol 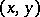 :
:
1) bilinearity: 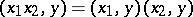 ,
,  ;
;
2) skew-symmetry: 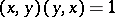 ;
;
3) non-degeneracy: 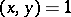 for all
for all 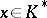 implies
implies 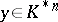 ;
; 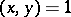 for all
for all 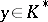 implies
implies 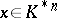 ;
;
4) if 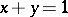 , then
, then 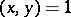 ;
;
5) if 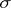 is an automorphism of
is an automorphism of 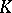 , then
, then
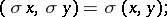 |
6) let 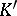 be a finite extension of
be a finite extension of  ,
, 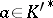 and
and 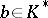 . Then
. Then
 |
where on the left-hand side the norm-residue symbol is regarded for 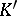 and on the right-hand side that for
and on the right-hand side that for 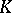 , and where
, and where 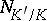 is the norm map from
is the norm map from 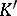 into
into 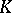 ;
;
7) 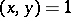 implies that
implies that 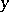 is a norm in the extension
is a norm in the extension 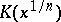 . (This explains the name of the symbol.)
. (This explains the name of the symbol.)
The function 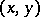 induces a non-degenerate bilinear pairing
induces a non-degenerate bilinear pairing
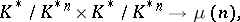 |
where 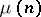 is the group of roots of unity generated by
is the group of roots of unity generated by 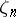 . Let
. Let 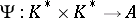 be a mapping into some Abelian group
be a mapping into some Abelian group  satisfying 1), 4) and the condition of continuity: For any
satisfying 1), 4) and the condition of continuity: For any 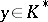 the set
the set 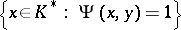 is closed in
is closed in  . The norm-residue symbol has the following universal property [3]: If
. The norm-residue symbol has the following universal property [3]: If  is the number of roots of unity in
is the number of roots of unity in 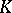 , then there exists a homomorphism
, then there exists a homomorphism 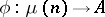 such that for any
such that for any 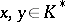 ,
,
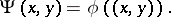 |
This property can serve as a basic axiomatic definition of the norm-residue symbol.
If 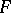 is a global field and
is a global field and 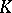 is the completion of
is the completion of 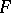 relative to a place
relative to a place  , then by the norm-residue symbol one also means the function
, then by the norm-residue symbol one also means the function 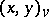 defined over
defined over 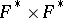 that is obtained by composition of the (local) norm-residue symbol
that is obtained by composition of the (local) norm-residue symbol 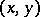 with the natural imbedding
with the natural imbedding 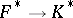 .
.
Often the norm-residue symbol is defined as an automorphism 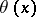 of the maximal Abelian extension of
of the maximal Abelian extension of 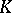 corresponding to an element
corresponding to an element  by local class field theory.
by local class field theory.
References
| [1] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [2] | H. Koch, "Galoissche Theorie der 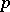 -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) |
| [3] | J.W. Milnor, "Introduction to algebraic 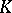 -theory" , Princeton Univ. Press (1971) -theory" , Princeton Univ. Press (1971) |
| [4] | I.R. Shafarevich, "A general reciprocity law" Mat. Sb. , 26 : 1 (1950) pp. 113–146 (In Russian) |
Comments
References
| [a1] | K. Iwasawa, "Local class field theory" , Oxford Univ. Press (1986) |
| [a2] | J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. 4, Sect. 8 |
Norm-residue symbol. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Norm-residue_symbol&oldid=12271