Watson transform

An integral transform 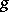of a function 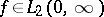, defined as follows:

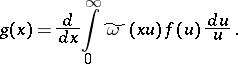(1)

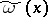Here is a real variable, the kernel has the form

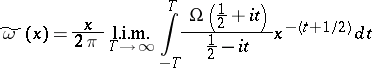(2)

(l.i.m. denotes the limit in the mean in 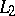) and the function 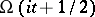satisfies the condition

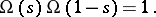The following conditions are sufficient for the existence of the kernel 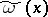and the inclusion :

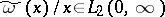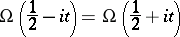and

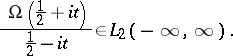For a function 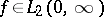, formula (1) defines the function 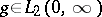almost-everywhere. The inversion formula for the Watson transform (1) has the form

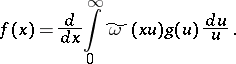Named after G.N. Watson [1], who was the first to study this transform.

References

[1]	G.N. Watson, "General transforms" Proc. London Math. Soc. (2) , 35 (1933) pp. 156–199

Comments

Quite generally, let 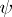be a Lebesgue-measure function in 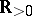and let

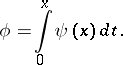The kernel 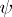(or ) is called a generalized kernel, or kernel of a generalized transform, if

a) 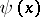is real valued on ;

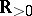b) ;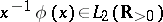

c) .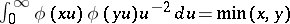

The operator 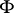defined on 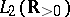by

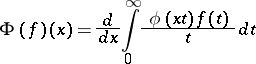is called a generalized transform or Watson transform.

References

[a1]	G.O. Okikiolu, "Aspects of the theory of bounded operators in 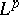-spaces" , Acad. Press (1971) pp. §6.7