Multiplicative arithmetic function

An arithmetic function of one argument, , satisfying the condition

(*)

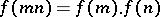for any pair of coprime integers . It is usually assumed that is not identically zero (which is equivalent to the condition 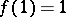). A multiplicative arithmetic function is called strongly multiplicative if for all prime numbers and all natural numbers 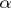. If (*) holds for any two numbers 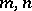, and not just for coprime numbers, then is called totally multiplicative; in this case .

Examples of multiplicative arithmetic functions. The function 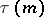, the number of natural divisors of a natural number ; the function , the sum of the natural divisors of the natural number 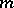; the Euler function 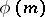; and the Möbius function 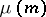. The function 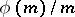is a strongly-multiplicative arithmetic function, a power function 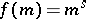is a totally-multiplicative arithmetic function.

Comments

The convolution product

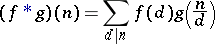yields a group structure on the multiplicative functions. The unit element is given by the function , where and for all . Another standard multiplicative function is the constant function ( 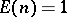for all 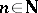) and its inverse 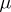, the Möbius function. Note that 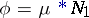, where 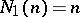for all , and that , .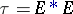

Formally, the Dirichlet series of a multiplicative function 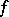has an Euler product:

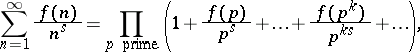whose form simplifies considerably if is strongly or totally multiplicative.

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1960) pp. Chapts. XVI-XVII