Whitney extension theorem
Let 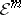 (respectively,
(respectively, 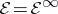 ) be the space of all
) be the space of all 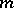 times differentiable (respectively, smooth) real-valued functions on
times differentiable (respectively, smooth) real-valued functions on 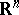 . Let
. Let 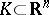 be compact. For a multi-index
be compact. For a multi-index 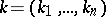 ,
, 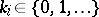 , let
, let 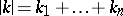 ,
, 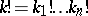 ,
, 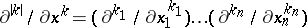 , and
, and 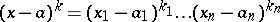 for
for 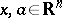 . The vector space
. The vector space 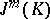 consists of all tuples
consists of all tuples  of continuous functions on
of continuous functions on 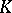 indexed by the multi-indices
indexed by the multi-indices 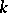 with
with 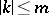 . For instance, if
. For instance, if 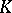 is a single point, then
is a single point, then 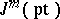 consists of sequences of
consists of sequences of 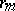 real numbers, where
real numbers, where 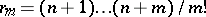 , and can be identified with the space of all polynomials of total degree
, and can be identified with the space of all polynomials of total degree 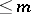 in
in  variables, and
variables, and 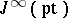 can be seen as the space of all power series in
can be seen as the space of all power series in  variables.
variables.
Let 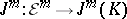 assign to
assign to  the
the 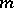 -jet of
-jet of 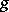 , i.e. the
, i.e. the 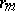 -tuple of continuous functions
-tuple of continuous functions 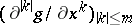 restricted to
restricted to 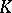 ; cf. also Jet. For each
; cf. also Jet. For each 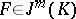 and
and 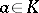 , let
, let  be the polynomial
be the polynomial
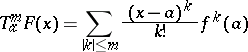 |
and let 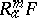 be the element
be the element
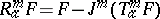 |
of 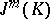 with components
with components 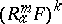 . The space
. The space 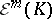 of functions differentiable in the sense of Whitney on
of functions differentiable in the sense of Whitney on 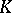 consists of those
consists of those 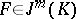 such that
such that
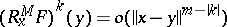 | (*) |
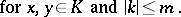 |
Of course, the elements of 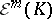 are not really functions, but that does no harm. If
are not really functions, but that does no harm. If 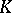 is a point,
is a point, 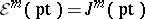 . The Whitney extension theorem now states that there exists a linear mapping
. The Whitney extension theorem now states that there exists a linear mapping 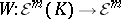 such that for every
such that for every 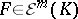 and every
and every 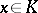 ,
,
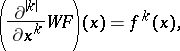 |
and such that 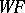 is smooth on
is smooth on 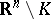 .
.
For 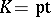 it follows that for every power series
it follows that for every power series 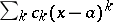 at
at  (in the variables
(in the variables 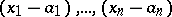 ) there is a smooth function on
) there is a smooth function on  whose Taylor series at
whose Taylor series at  is precisely this power series.
is precisely this power series.
This results also (by induction on the number of variables) from the Borel extension lemma. Let 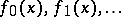 be a series of smooth functions defined on a neighbourhood of
be a series of smooth functions defined on a neighbourhood of 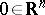 . Then there is a smooth function
. Then there is a smooth function 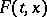 defined on a neighbourhood of
defined on a neighbourhood of 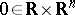 such that
such that 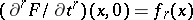 for all
for all  .
.
References
| [a1] | H. Whitney, "Analytic extensions of differentiable functions defined in closed sets" Trans. Amer. Math. Soc. , 36 (1934) pp. 63–89 |
| [a2] | B. Malgrange, "Ideals of differentiable functions" , Oxford Univ. Press (1966) pp. Chapt. I |
| [a3] | J.C. Tougeron, "Ideaux de fonction différentiables" , Springer (1972) pp. Chapt. IV |
| [a4] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) pp. 108ff |
Whitney extension theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitney_extension_theorem&oldid=11936