Harmonic measure
A concept in the theory of harmonic functions (cf. Harmonic function) connected with estimating the modulus of an analytic function inside a domain if certain bounds on the modulus on the boundary of the domain are known [1], [2]. Let 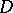 be a bounded open set in the Euclidean space
be a bounded open set in the Euclidean space 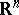 ,
, 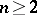 ; let
; let 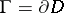 be the boundary of
be the boundary of  ; and let
; and let  be a finite real-valued continuous function on
be a finite real-valued continuous function on 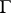 . To each such function
. To each such function 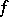 there corresponds a unique harmonic function
there corresponds a unique harmonic function 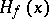 on
on 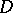 which, for
which, for  , is a generalized solution of the Dirichlet problem. If the point
, is a generalized solution of the Dirichlet problem. If the point  is assumed to be fixed, the functional
is assumed to be fixed, the functional  will define on the compact set
will define on the compact set 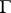 a positive Radon measure
a positive Radon measure 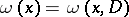 , which is called the harmonic measure at the point
, which is called the harmonic measure at the point  . The formula for the representation of the generalized solution of the Dirichlet problem,
. The formula for the representation of the generalized solution of the Dirichlet problem,
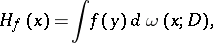 |
obtained by Ch.J. de la Vallée-Poussin by the balayage method, is valid for all functions 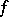 which are continuous on
which are continuous on 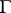 . Moreover, if
. Moreover, if 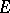 is an arbitrary Borel set on
is an arbitrary Borel set on 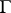 , the harmonic measure
, the harmonic measure 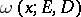 ,
, 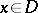 , of
, of 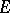 at
at  is equal to the value at
is equal to the value at  of the generalized solution of the Dirichlet problem for the characteristic function
of the generalized solution of the Dirichlet problem for the characteristic function 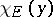 ,
, 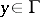 , of
, of 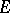 .
.
The basic properties of a harmonic measure are: 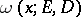 is a harmonic function of the point
is a harmonic function of the point  in
in 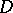 ;
;
 |
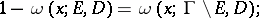 |
if 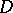 is a domain and
is a domain and  even at a single point
even at a single point 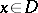 , then
, then 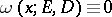 .
.
In the last-named case 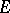 is known as a set of harmonic measure zero. If a compact set
is known as a set of harmonic measure zero. If a compact set 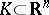 has harmonic measure zero with respect to some domain
has harmonic measure zero with respect to some domain 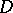 ,
, 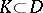 , i.e.
, i.e. 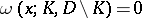 , then it has harmonic measure zero with respect to all other domains, i.e.
, then it has harmonic measure zero with respect to all other domains, i.e.  is a set of absolute harmonic measure zero. A set
is a set of absolute harmonic measure zero. A set  has absolute harmonic measure zero if and only if it has zero (harmonic) capacity.
has absolute harmonic measure zero if and only if it has zero (harmonic) capacity.
As regards applications to the theory of functions of a complex variable, the dependence of a harmonic measure on the domain 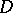 is of special importance. This dependence is expressed by the principle of harmonic measure (cf. Harmonic measure, principle of), which states that a harmonic measure does not decrease under mappings of the domain
is of special importance. This dependence is expressed by the principle of harmonic measure (cf. Harmonic measure, principle of), which states that a harmonic measure does not decrease under mappings of the domain 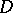 realized by univalent analytic functions
realized by univalent analytic functions  ,
,  . In particular, a harmonic measure remains unchanged under a one-to-one conformal mapping.
. In particular, a harmonic measure remains unchanged under a one-to-one conformal mapping.
Explicit computations of harmonic measures are possible only for the simplest domains  (mainly for the disc, for the sphere, for a half-plane, and for a half-space; see Poisson integral). This is the reason for the importance of the various estimation methods for harmonic measure [4], [5], [6], [7], which are mainly based on the principle of extension of domain (cf. Extension of domain, principle of). In the simplest form, for
(mainly for the disc, for the sphere, for a half-plane, and for a half-space; see Poisson integral). This is the reason for the importance of the various estimation methods for harmonic measure [4], [5], [6], [7], which are mainly based on the principle of extension of domain (cf. Extension of domain, principle of). In the simplest form, for 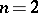 , this principle consists in the following: Let a finitely-connected domain
, this principle consists in the following: Let a finitely-connected domain 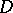 be bounded by a finite number of Jordan curves
be bounded by a finite number of Jordan curves 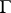 and let
and let 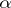 be an arc on
be an arc on 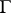 . Then, if the domain
. Then, if the domain  is extended in some way across the complementary part
is extended in some way across the complementary part 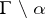 of the boundary, the harmonic measure
of the boundary, the harmonic measure  can only increase.
can only increase.
References
| [1] | T. Carleman, "Sur les fonctions inverses des fonctions entières d'ordre fini" Ark. Mat. , 15 : 10 (1921) pp. 1–7 |
| [2] | F. Nevanlinna, R. Nevanlinna, "Ueber die Eigenschaften einer analytischen Funktion in der Umgebung einer singulären Stelle oder Linie" Acta Soc. Sci. Fennica , 50 : 5 (1922) pp. 1–46 |
| [3] | Ch.J. de la Vallée-Poussin, Ann. Inst. H. Poincaré , 2 (1932) pp. 169–232 |
| [4] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [5] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [6] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [7] | K. Haliste, "Estimates of harmonic measure" Ark. Mat. , 6 : 1 (1965) pp. 1–31 |
Comments
Harmonic measure is an important tool in axiomatic potential theory (cf. Potential theory, abstract), see [a1].
For domains in 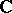 very precise estimates for harmonic measure in terms of Hausdorff measure have been obtained recently. Let
very precise estimates for harmonic measure in terms of Hausdorff measure have been obtained recently. Let 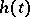 be a continuous increasing function for
be a continuous increasing function for 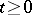 ,
, 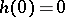 , and let
, and let 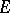 be a Borel set. Let
be a Borel set. Let 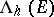 denote the Hausdorff measure with respect to
denote the Hausdorff measure with respect to 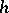 of
of 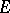 . Let
. Let 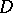 be a domain in
be a domain in 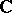 and set
and set 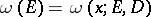 . Makarov's theorems [a3] are: 1) Suppose that
. Makarov's theorems [a3] are: 1) Suppose that  is simply connected. If
is simply connected. If 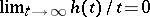 , then
, then 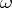 is singular with respect to
is singular with respect to  , i.e.
, i.e. 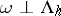 . 2) There exist constants
. 2) There exist constants  ,
,  with the following property: Let
with the following property: Let
 |
Then for every Jordan domain 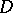 ,
, 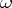 is absolutely continuous with respect to
is absolutely continuous with respect to 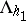 , i.e.
, i.e.  . However, there exists a Jordan domain
. However, there exists a Jordan domain 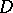 with
with  .
.
Next (B. Øksendal, Jones, Wolff): If  , then for every domain
, then for every domain 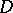 in
in 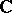 ,
, 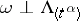 .
.
References
| [a1] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [a2] | J.B. Garnett, "Applications of harmonic measure" , Wiley (Interscience) (1986) |
| [a3] | N. Makarov, "On the distortion of boundary sets under conformal mappings" Proc. London Math. Soc. , 51 (1985) pp. 369–384 |
Harmonic measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonic_measure&oldid=11907