Universe
From Encyclopedia of Mathematics
A set  which is closed under the formation of unions, singletons, subelements, power sets, and pairs; more precisely:
which is closed under the formation of unions, singletons, subelements, power sets, and pairs; more precisely:
1)  ,
,  implies
implies  ;
;
2)  implies
implies  ;
;
3)  implies
implies  ;
;
4)  implies
implies 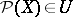 ;
;
5) 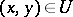 if and only if
if and only if  .
.
The existence of infinite universes in axiomatic set theory is equivalent to the existence of strongly inaccessible cardinals (cf. Cardinal number). A universe is a model for Zermelo–Fraenkel set theory. Universes were introduced by A. Grothendieck in the context of category theory in order to introduce the "set" of natural transformations of functors between (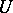 -) categories, and in order to admit other "large" category-theoretic constructions.
-) categories, and in order to admit other "large" category-theoretic constructions.
References
| [a1] | J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) ((especially the article of D.A. Martin on Descriptive set theory)) |
| [a2] | P. Gabriel, "Des catégories abéliennes" Bull. Soc. Math. France , 90 (1962) pp. 323–448 |
| [a3] | K. Kunen, "Set theory" , North-Holland (1980) |
How to Cite This Entry:
Universe. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universe&oldid=11866
Universe. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universe&oldid=11866
This article was adapted from an original article by B. Pareigis (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article