Universe

A set which is closed under the formation of unions, singletons, subelements, power sets, and pairs; more precisely:

1) , implies ;

2) implies ;

3) implies ;

4) implies ;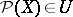

5) 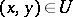if and only if .

The existence of infinite universes in axiomatic set theory is equivalent to the existence of strongly inaccessible cardinals (cf. Cardinal number). A universe is a model for Zermelo–Fraenkel set theory. Universes were introduced by A. Grothendieck in the context of category theory in order to introduce the "set" of natural transformations of functors between (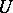-) categories, and in order to admit other "large" category-theoretic constructions.

References

[a1]	J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) ((especially the article of D.A. Martin on Descriptive set theory))
[a2]	P. Gabriel, "Des catégories abéliennes" Bull. Soc. Math. France , 90 (1962) pp. 323–448
[a3]	K. Kunen, "Set theory" , North-Holland (1980)