Prime ideal(2)

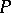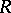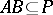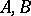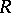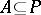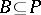A two-sided ideal of a ring such that , where are ideals of , implies either or . For an associative ring the following is an equivalent definition in terms of elements:

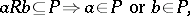where 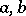are elements in . Every primitive ideal is a prime ideal.

Let 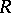be an associative-commutative ring with an identity. Then an ideal 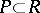is prime if and only if 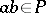implies 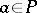or 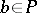, i.e. if and only if the quotient ring is an integral domain. In this case every maximal ideal is prime and the intersection of all prime ideals is the radical of the null ideal (i.e. is the set of nilpotent elements).

A generalization of the concept of a prime ideal is that of a primary ideal. In the theory of primary decomposition, the prime ideals play the same role as the prime numbers do in the decomposition of integers in powers of prime numbers, while the primary ideals play the role of powers of prime numbers.

An ideal 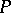in a lattice 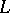is called prime if

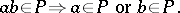An ideal 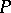is prime if and only if 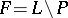is a prime filter, i.e. if 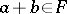implies 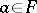or .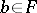

References

[1]	N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)
[2]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)
[3]	O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975)
[4]	L.A. Skornyakov, "Elements of lattice theory" , A. Hilger (1977) (Translated from Russian)