Spectral operator
spectral measure
A bounded linear operator  mapping a Banach space
mapping a Banach space  into itself and such that for the
into itself and such that for the 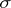 -algebra
-algebra 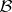 of Borel subsets
of Borel subsets 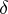 in the plane there is a resolution of the identity
in the plane there is a resolution of the identity 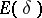 with the following properties: 1) for any
with the following properties: 1) for any  the projector
the projector 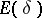 reduces
reduces 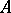 , that is,
, that is, 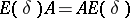 and the spectrum
and the spectrum 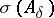 lies in
lies in 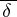 , where
, where 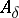 is the restriction of
is the restriction of 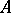 to the invariant subspace
to the invariant subspace  ; 2) the mapping
; 2) the mapping 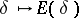 is a homeomorphism of
is a homeomorphism of 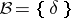 into the Boolean algebra
into the Boolean algebra 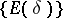 ; 3) all projectors
; 3) all projectors 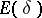 are bounded, that is,
are bounded, that is,  ,
, 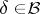 ; and 4) the resolution of the identity
; and 4) the resolution of the identity  is countably additive in the strong topology of
is countably additive in the strong topology of 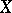 , that is, for any
, that is, for any 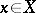 and any sequence
and any sequence 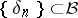 of pairwise disjoint sets,
of pairwise disjoint sets,
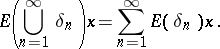 |
The concept of a spectral operator can be generalized to the case of closed unbounded operators. In 1), the additional requirement is then that the inclusion 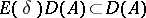 holds, where
holds, where 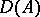 is the domain of definition of
is the domain of definition of 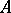 , and
, and 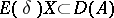 for bounded
for bounded 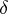 .
.
All linear operators on a finite-dimensional space and all self-adjoint and normal operators on a Hilbert space are spectral operators. For example, the operator
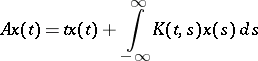 |
on 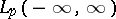 ,
, 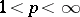 , is spectral on
, is spectral on
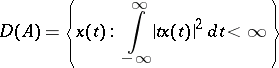 |
if the kernel 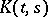 is the Fourier transform of a Borel measure
is the Fourier transform of a Borel measure 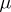 on the plane of total variation
on the plane of total variation 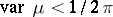 and is such that
and is such that
 |
are bounded linear operators on 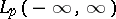 .
.
Spectral operators have many important properties, such as:
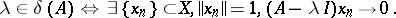 |
If 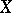 is separable, the point and residual spectra of
is separable, the point and residual spectra of  are at most countable.
are at most countable.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral operators" , 3 , Interscience (1971) |
| [2] | N. Dunford, "A survey of the theory of spectral operators" Bull. Amer. Math. Soc. , 64 (1958) pp. 217–274 |
Spectral operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_operator&oldid=11778