Bernstein algebra
Around 1900, S.N. Bernstein (cf. [a3], [a4], [a5]) worked on an important problem concerning the laws of formal genetics. This problem is known today as the Bernstein problem. Following Yu.I. Lyubich (cf. [a10]), this problem can be expressed as follows. The state of a population in a given generation is described by a vector in  whose coordinates satisfy
whose coordinates satisfy  (
( ) and
) and  . The set
. The set  of all states is a simplex in
of all states is a simplex in  and the vertices
and the vertices  (
(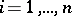 ) of
) of  are the different types of individuals in the population. If
are the different types of individuals in the population. If 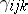 is the probability that an individual
is the probability that an individual 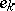 appears in the next generation from parents of types
appears in the next generation from parents of types 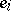 and
and 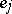 , then
, then 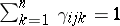 (
(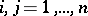 ) and
) and  (
(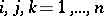 ). In absence of selection and under random hypothesis, the state of the population in the next generation can be written, in terms of coordinates, as
). In absence of selection and under random hypothesis, the state of the population in the next generation can be written, in terms of coordinates, as 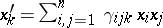 (
(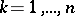 ). These relations define a quadratic operator
). These relations define a quadratic operator 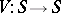 called the evolutionary quadratic operator. The Bernstein stationarity principle says that
called the evolutionary quadratic operator. The Bernstein stationarity principle says that 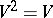 and the Bernstein problem aims at describing all quadratic operators satisfying this principle. Bernstein solved his problem for
and the Bernstein problem aims at describing all quadratic operators satisfying this principle. Bernstein solved his problem for 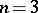 and much progress was achieved recently (cf. [a6], [a8]) in this direction. The Bernstein problem can be translated in terms of algebra structure. In fact, over
and much progress was achieved recently (cf. [a6], [a8]) in this direction. The Bernstein problem can be translated in terms of algebra structure. In fact, over 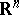 an algebra structure can be defined via the operator
an algebra structure can be defined via the operator 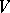 by
by
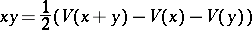 |
for all 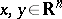 , and if
, and if 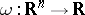 is the mapping defined by
is the mapping defined by 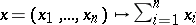 , then
, then 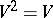 if and only if
if and only if 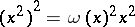 for all
for all  . Moreover,
. Moreover, 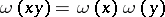 for all
for all 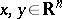 . Of course, to define this multiplication over the whole space
. Of course, to define this multiplication over the whole space 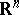 starting from the simplex
starting from the simplex 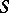 , one has to make convenient extensions of this multiplication by bilinearity. Now, in general, if
, one has to make convenient extensions of this multiplication by bilinearity. Now, in general, if 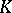 is a (commutative) field and
is a (commutative) field and 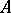 is a commutative
is a commutative 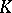 -algebra, then a weighted algebra
-algebra, then a weighted algebra 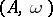 over
over 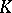 is said to be a Bernstein algebra if
is said to be a Bernstein algebra if  for all
for all 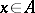 (cf. [a2]). In recent years (1990s), the theory of Bernstein algebras has been substantially improved. V.M. Abraham (cf. [a1]) suggests the construction of a generalized Bernstein algebra. In this perspective, for an element
(cf. [a2]). In recent years (1990s), the theory of Bernstein algebras has been substantially improved. V.M. Abraham (cf. [a1]) suggests the construction of a generalized Bernstein algebra. In this perspective, for an element 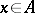 , where
, where 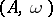 is a weighted algebra, the plenary powers
is a weighted algebra, the plenary powers 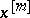 of
of  are defined by
are defined by 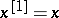 and
and 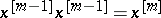 for all integer
for all integer 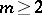 . The plenary powers can be interpreted by saying that they represent random mating between discrete non-overlapping generations.
. The plenary powers can be interpreted by saying that they represent random mating between discrete non-overlapping generations. 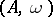 is called an
is called an  th order Bernstein algebra if
th order Bernstein algebra if 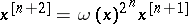 for all
for all 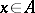 , where
, where 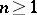 is the smallest such integer (cf. [a11]). Second-order Bernstein algebras are simply called Bernstein algebras and first-order Bernstein algebras are also called gametic diploid algebras. The interpretation of the equation
is the smallest such integer (cf. [a11]). Second-order Bernstein algebras are simply called Bernstein algebras and first-order Bernstein algebras are also called gametic diploid algebras. The interpretation of the equation 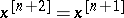 (
( such that
such that 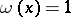 ) is that equilibrium in the population is reached after exactly
) is that equilibrium in the population is reached after exactly  generations of intermixing. For genetic properties of Bernstein algebras, see [a7] and [a12].
generations of intermixing. For genetic properties of Bernstein algebras, see [a7] and [a12].
See also Genetic algebra; Baric algebra.
References
| [a1] | V.M. Abraham, "Linearising quadratic transformations in genetic algebras" Thesis, Univ. London (1975) |
| [a2] | M.T. Alcalde, C. Burgueno, A. Labra, A. Micali, "Sur les algèbres de Bernstein" Proc. London Math. Soc. (3) , 58 (1989) pp. 51–68 |
| [a3] | S.N. Bernstein, "Principe de stationarité et généralisation de la loi de Mendel" C.R. Acad. Sci. Paris , 177 (1923) pp. 528–531 |
| [a4] | S.N. Bernstein, "Démonstration mathématique de la loi d'hérédité de Mendel" C.R. Acad. Sci. Paris , 177 (1923) pp. 581–584 |
| [a5] | S.N. Bernstein, "Solution of a mathematical problem connected with the theory of heredity" Ann. Math. Stat. , 13 (1942) pp. 53–61 |
| [a6] | S. González, J.C. Gutiérrez, C. Martínez, "The Bernstein problem in dimension  " J. Algebra , 177 (1995) pp. 676–697 " J. Algebra , 177 (1995) pp. 676–697 |
| [a7] | A.N. Griskhov, "On the genetic property of Bernstein algebras" Soviet Math. Dokl. , 35 (1987) pp. 489–492 (In Russian) |
| [a8] | J.C. Gutiérrez, "The Bernstein problem for type 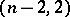 " J. Algebra , 181 (1996) pp. 613–627 " J. Algebra , 181 (1996) pp. 613–627 |
| [a9] | P. Holgate, "Genetic algebras satisfying Bernstein's stationarity principle" J. London Math. Soc. (2) , 9 (1975) pp. 613–623 |
| [a10] | Yu.I. Lyubich, "Mathematical structures in population genetics" Biomathematics , 22 (1992) |
| [a11] | C. Mallol, A. Micali, M. Ouattara, "Sur les algèbres de Bernstein IV" Linear Alg. & Its Appl. , 158 (1991) pp. 1–26 |
| [a12] | A. Micali, M. Ouattara, "Structure des algèbres de Bernstein" Linear Alg. & Its Appl. , 218 (1995) pp. 77–88 |
Bernstein algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_algebra&oldid=11704