Integer
See Number.
Comments
An integer is an element of the ring of integers  . The ring
. The ring 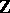 is the minimal ring which extends the semi-ring of natural numbers
is the minimal ring which extends the semi-ring of natural numbers  , cf. Natural number. Cf. Number for an axiomatic characterization of
, cf. Natural number. Cf. Number for an axiomatic characterization of  .
.
In algebraic number theory the term integer is also used to denote elements of an algebraic number field that are integral over 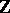 . I.e. if
. I.e. if 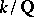 is an algebraic field extension, where
is an algebraic field extension, where 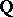 is the field of rational numbers, the field of fractions of
is the field of rational numbers, the field of fractions of 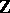 , then the integers of
, then the integers of  are the elements of the integral closure of
are the elements of the integral closure of 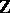 in
in 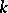 , cf. Integral extension of a ring.
, cf. Integral extension of a ring.
The integers of the algebraic number field 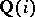 ,
, 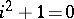 , are the elements
, are the elements 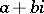 ,
, 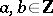 . They are called the Gaussian integers.
. They are called the Gaussian integers.
Let 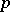 be a prime number. A
be a prime number. A  -adic integer is an element of
-adic integer is an element of 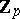 , the closure of
, the closure of  in the field
in the field 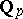 of
of 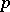 -adic numbers. The field
-adic numbers. The field 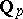 is the topological completion of the field
is the topological completion of the field 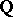 for the
for the  -adic topology on
-adic topology on 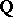 which is defined by the non-Archimedean norm
which is defined by the non-Archimedean norm
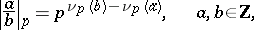 |
where 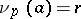 if
if 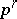 divides
divides  and
and  does not divide
does not divide  , and
, and 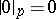 .
.
References
| [a1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1975) (Translated from Russian) (German translation: Birkhäuser, 1966) |
Integer. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integer&oldid=11339