Snake-like continuum
A continuum which, for any 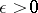 , admits an open covering whose nerve (cf. Nerve of a family of sets) is a finite linear complex. In other words, for any
, admits an open covering whose nerve (cf. Nerve of a family of sets) is a finite linear complex. In other words, for any 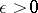 the continuum must be covered by a finite system
the continuum must be covered by a finite system 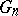 ,
, 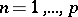 , of open sets such that the diameter of each
, of open sets such that the diameter of each 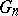 is less than
is less than  and
and 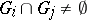 if and only if
if and only if 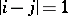 (such a system is called an
(such a system is called an  -chain). Every snake-like continuum is irreducible (see Irreducible continuum) between any pair of its points. Every subcontinuum of a snake-like continuum is snake-like. Two hereditarily-indecomposable snake-like continua (see Indecomposable continuum) containing more than one point are homeomorphic; these are known as pseudo-arcs (cf. Pseudo-arc). Every snake-like continuum is topologically imbeddable in the plane. Any homogeneous snake-like continuum is a pseudo-arc. Every snake-like continuum is the continuous image of a pseudo-arc and the limit of the inverse spectrum of arcs.
-chain). Every snake-like continuum is irreducible (see Irreducible continuum) between any pair of its points. Every subcontinuum of a snake-like continuum is snake-like. Two hereditarily-indecomposable snake-like continua (see Indecomposable continuum) containing more than one point are homeomorphic; these are known as pseudo-arcs (cf. Pseudo-arc). Every snake-like continuum is topologically imbeddable in the plane. Any homogeneous snake-like continuum is a pseudo-arc. Every snake-like continuum is the continuous image of a pseudo-arc and the limit of the inverse spectrum of arcs.
References
| [1] | K. Kuratowski, "Topology" , 2 , Acad. Press (1968) (Translated from French) |
Comments
A snake-like continuum is also called a chainable continuum.
Snake-like continuum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Snake-like_continuum&oldid=11338