Bessel polynomials

Related to Bessel functions, [a2], the Bessel polynomials satisfy

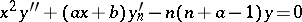and are given by

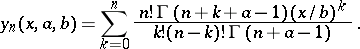The ordinary Bessel polynomials are those found with , [a2].

The moments associated with the Bessel polynomials satisfy

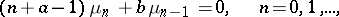and are given by .

The weight equation is

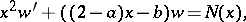where is any function with moments. This equation has been solved when

where

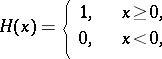when (no restriction), and , [a3]. The weight for the ordinary Bessel polynomials was found by S.S. Kim, K.H. Kwon and S.S. Han, [a1], after over 40 years of search.

Using the three-term recurrence relation

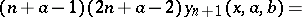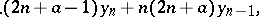the norm square is easily calculated and equals , [a2], where 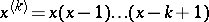. Clearly, 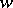generates a Krein space on .

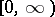References

[a1]	S.S. Kim, K.H. Kwon, S.S. Han, "Orthogonalizing weights of Tchebychev sets of polynomials" Bull. London Math. Soc. , 24 (1992) pp. 361–367
[a2]	H.L. Krall, O. Frink, "A new class of orthogonal polynomials: The Bessel polynomials" Trans. Amer. Math. Soc. , 63 (1949) pp. 100–115
[a3]	P. Maroni, "An integral representation for the Bessel form" J. Comp. Appl. Math. , 57 (1995) pp. 251–260