Iwasawa decomposition

The unique representation of an arbitrary element $ g $ of a non-compact connected semi-simple real Lie group $ G $ as a product $ g = k an $ of elements $ k,\ a,\ n $ of analytic subgroups $ K,\ A,\ N $ , respectively, where $ K $ , $ A $ and $ N $ are defined as follows. Let $ \mathfrak g = \mathfrak k + \mathfrak P $ be a Cartan decomposition of the Lie algebra $ \mathfrak g $ of $ G $ ; let $ \mathfrak a $ be the maximal commutative subspace of the space $ \mathfrak P $ , and let $ \mathfrak N $ be a nilpotent Lie subalgebra of $ \mathfrak g $ such that $ \mathfrak N $ is the linear hull of the root vectors in some system of positive roots with respect to $ \mathfrak a $ . The decomposition of the Lie algebra as the direct sum of the subalgebras $ \mathfrak k $ , $ \mathfrak a $ and $ \mathfrak N $ is called the Iwasawa decomposition [1] of the semi-simple real Lie algebra $ \mathfrak g $ . The groups $ K $ , $ A $ and $ N $ are defined to be the analytic subgroups of $ G $ corresponding to the subalgebras $ \mathfrak k $ , $ \mathfrak a $ and $ \mathfrak N $ , respectively. The groups $ K $ , $ A $ and $ N $ are closed; $ A $ and $ N $ are simply-connected; $ K $ contains the centre of $ G $ , and the image of $ K $ under the adjoint representation of $ G $ is a maximal compact subgroup of the adjoint group of $ G $ . The mapping $ (k,\ a,\ n) \rightarrow kan $ is an analytic diffeomorphism of the manifold $ K \times A \times N $ onto the Lie group $ G $ . The Iwasawa decomposition plays a fundamental part in the representation theory of semi-simple Lie groups. The Iwasawa decomposition can be defined also for connected semi-simple algebraic groups over a $ p $ - adic field (or, more generally, for groups of $ p $ - adic type) (see [4], [5]).

References

[1]	K. Iwasawa, "On some types of topological groups" Ann. of Math. , 50 (1949) pp. 507–558 MR0029911 Zbl 0034.01803
[2]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) MR0793377 Zbl 0484.22018
[3]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) MR0514561 Zbl 0451.53038
[4]	F. Bruhat, "Sur une classe de sous-groupes compacts maximaux des groupes de Chevalley sur un corps 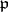-adique" Publ. Math. IHES , 23 (1964) pp. 45–74 MR179298
[5]	N. Iwahori, H. Matsumoto, "On some Bruhat decomposition and the structure of the Hecke rings of 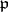-adic Chevalley groups" Publ. Math. IHES , 25 (1965) pp. 5–48 MR185016

Comments

An example of an Iwasawa decomposition is $ \mathop{\rm SL}\nolimits _{n} ( \mathbf R ) = K A N $ with $ K = \mathop{\rm SO}\nolimits _{n} ( \mathbf R ) $ , $ A $ the subgroup of diagonal matrices of $ \mathop{\rm SL}\nolimits _{n} ( \mathbf R ) $ and $ N $ a lower triangular matrix with $ 1 $ ' s on the diagonal. So, in particular, every element of $ \mathop{\rm SL}\nolimits _{n} ( \mathbf R ) $ gets written as a product of a special orthogonal matrix and a lower triangular matrix.

References

[a1]	S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4 MR0754767 Zbl 0543.58001