Average-case computational complexity

The efficiency of an algorithm $\mathcal{A}$ is measured by the amount of computational resources used, in the first place time (number of computation steps) and space (amount of memory cells). These values may depend on the individual inputs given to $\mathcal{A}$. Thus, in general it is infeasible to give a complete description of the efficiency of an algorithm, simply because the amount of data grows exponentially with respect to the size of the inputs.

Traditionally, one has considered the so-called worst-case complexity, which for each input size $n$ determines the maximum amount of resources used by $\mathcal{A}$ on any input of that size. This conservative estimation provides a guaranteed upper bound, but in specific cases may be much too pessimistic. The simplex algorithm is a well-known example that is heavily used in practice since it tends to find a solution very fast [a3]. In the worst case, however, it requires an exponential amount of time [a12].

To estimate the average-case behaviour of an algorithm precisely is quite a difficult task in general. Only few examples are known where this has been achieved so far (as of 2000; compare [a6]). Quick-sort is one of the most extensively investigated algorithms. To sort $n$ data items, it shows a quadratic worst-case and a $\Theta( n \operatorname { log } n )$ average-case time complexity [a22]. For a more detailed analysis of its running time beyond the expectation, see [a21]. These results have been shown for the uniform distribution, where every permutation of the input data is equally likely. For biased distributions, the analysis becomes significantly more complicated, and for arbitrary distributions the claim is no longer true. The average-case behaviour of standard quick-sort decreases significantly if the input sequence tends to be partially presorted. See below for more details on the influence of the distribution.

To determine the average-case complexity of an algorithmic problem $\mathcal{Q}$, i.e. to find the "best" algorithm for $\mathcal{Q}$ with respect to the average utilization of its resources, is even harder. The sorting problem is one of the rare positive exceptions, since a matching lower bound can be derived by an information-theoretic argument almost as simple as for the worst case. Again, the lower bound only holds for the uniform distribution; for arbitrary distributions it has to be replaced by their entropy.

For most problems that are believed not to be efficiently solvable in the worst case, for example the $\cal N P$-complete ones (cf. also Computational complexity classes; Complexity theory; $\cal N P$), little is known about their average-case complexity. For example, for SAT, the satisfiability problem for Boolean formulas in conjunctive normal form, quite a large variation of behaviour has been observed for different satisfiability algorithms (for an overview, see [a19]). For certain distributions they perform quite well, but the question arises what are "reasonable" or "typical" distributions. Similar behaviour occurs for combinatorial optimization problems based on graphs if the distribution is given according to the random graph model [a5]. For example, if the edge probability is not extremely small, the $\cal N P$-complete problems "3-colourability" and "Hamiltonian circuit" can easily be solved, simply because almost-all such random graphs contain a Hamiltonian circuit and also a $4$-clique, thus cannot be $3$-coloured [a2], [a7].

For SAT the relation between the number of clauses and the number of variables seems to be most important: with few clauses a random formula has a lot of satisfying assignments which can be found quickly. On the other hand, many clauses are likely to make a random formula unsatisfiable and there is a good chance that a proof for this property can be deduced fast. For SAT there is no simple notion of a uniform distribution, but there exists a critical relation between the number of clauses and variables, for which a random formula fulfilling this relation is equally likely to be satisfiable or unsatisfiable. It has been conjectured that this boundary behaves like a phase transition with a numerical value around $4.2$, like it is known for properties of random graphs [a17], [a13]. For distributions in this range the average-case complexity of SAT is still unresolved (as of 2000; see also [a14]).

Complexity estimations have to be based on a precise machine model. For static models like straight-line programs, all inputs of a given size are treated by the same sequence of operations, thus there is no difference in the running time. Boolean circuits seem to behave similarly if one measures the length of the computation simply by the circuit depth. However, a dynamic notion of delay has been established such that for different inputs the results of the computation are available at different times [a9]. Thus, the average-case behaviour is not identical to the worst-case behaviour — an average-case analysis makes sense. A precise complexity estimation has been given for many Boolean functions, exhibiting in some cases a provable exponential speed-up of the average-case complexity in comparison to the worst-case complexity [a11]. This holds for a wide range of distributions. The complexity for generating the distributions has a direct influence on the average-case behaviour of circuits.

If one bases the complexity analysis on machine models like the Turing machine or the random access machine (RAM), the situation gets even more complicated. In contrast to the circuit model, where for each circuit the number of input bits it can handle is fixed — thus a family of circuits is needed for different input sizes —, now a single machine can treat inputs of arbitrary length. Hence, there are two kinds of degree to which one can average the behaviour of an algorithm. First, for each $n$ one could measure the expected runtime given a probability distribution $\mu _ { n }$ on the set of all inputs of size $n$. Thus, for each input size $n$, a corresponding distribution is required. One then requires that this expectation as a function of $n$ is majorized by a desired complexity bound, like a linear or polynomial function. A more general approach would be to have a single probability distribution $\mu$ defined over the whole input space. Then one could also weight different input sizes — not all values of $n$ have to be equally important.

It has been observed that there exists a universal distribution that makes the average-case complexity of any algorithm as bad as its worst-case complexity up to a constant factor [a15]. Such distributions are called malign. Fortunately, the universal distribution is not computable, i.e. there does not exist a mechanical procedure to generate input instances according to this distribution. Thus, this universally bad distribution will probably not occur "in real life" . From these results one can infer that an average-case analysis has to take the underlying distribution carefully into account and that a significantly better average-case behaviour can only be expected for computationally simple distributions. A simple notion for this purpose is polynomial-time computability [a16]. It requires that given a (natural) linear ordering $X _ { 1 } , X _ { 2 } , \dots$ on the problem instances, the aggregated probability $\hat{\mu}$ of a distribution with density function $\mu$ (cf. also Density of a probability distribution) can be computed in polynomial time ($\hat { \mu } ( X _ { i } ) = \sum _ { X _ { j } \leq X _ { i } } \mu ( X _ { j } )$). Finer differentiations are discussed in [a1], [a18], [a20], [a10]. From a global distribution $\mu$ one can derive its normalized restriction $\mu _ { n }$ to inputs $X$ of length $n$ as $\mu _ { n } ( X ) : = \mu ( X ) / \sum _ { |Y| = n } \mu ( Y )$.

For most algorithmic problems, already the worst-case complexity has not yet been determined precisely. But a lot of relative classifications are known, comparing the complexity of one problem to that of another problem. This is obtained by reductions between problems. Useful here are many-one reductions, i.e. mappings $\rho$ from instances $X _ { 1 }$ for a problem ${\cal Q} _ { 1 }$ to instances $X _ { 2 }$ of a problem ${\cal Q}_2$, such that from the instance $\rho ( X _ { 1 } )$ for ${\cal Q}_2$ and its solution with respect to ${\cal Q}_2$ one can easily deduce a solution for $X _ { 1 }$ with respect to ${\cal Q} _ { 1 }$. In the case of decision problems, for example, where for every instance the answer is either "yes" or "no" , one simply requires that $\rho ( X _ { 1 } )$ has the same answer as $X _ { 1 }$. Thus, an algorithm solving ${\cal Q}_2$ together with a reduction from ${\cal Q} _ { 1 }$ to ${\cal Q}_2$ can be used to solve ${\cal Q} _ { 1 }$. In order to make this transformation meaningful, the reduction itself should be of lower complexity than ${\cal Q} _ { 1 }$ and ${\cal Q}_2$. Then one can infer that ${\cal Q} _ { 1 }$ is at most as difficult as ${\cal Q}_2$. Polynomial-time many-one reductions require that the function $\rho$ can be computed in polynomial time. They play a central role in complexity analysis, since the class $\mathcal{P}$, polynomial time complexity, is a very robust notion to distinguish algorithmic problems that are feasibly solvable from the intractable ones. To investigate the complexity classes $\mathcal{C}$ above $\mathcal{P}$, a problem $\mathcal{Q}$ in $\mathcal{C}$ with the property that all problems in this class can be reduced to $\mathcal{Q}$ is called complete for $\mathcal{C}$. Such a $\mathcal{Q}$ can be considered as a hardest problem in $\mathcal{C}$ — an efficient solution of $\mathcal{C}$ would yield efficient solutions for all other problems in this class. Complete problems capture the intrinsic complexity of a class.

This methodology has been established well for worst-case complexity. When trying to apply it to the average case, one faces several technical difficulties. Now one has to deal with pairs, consisting of a problem $\mathcal{Q}$ and a distribution $\mu$ for $\mathcal{Q}$, called distributional problems. A meaningful reduction between such problems $( \mathcal{Q} _ { 1 } , \mu _ { 1 } )$ and $( {\cal Q} _ { 2 } , \mu _ { 2 } )$ has to make sure that likely instances of ${\cal Q} _ { 1 }$ are mapped to likely instances of ${\cal Q}_2$, a property called dominance [a16]. Secondly, polynomial on average time complexity cannot simply be defined by taking the expectation, which would mean that for an algorithm $\mathcal{A}$ with individual running times $\text{time}_\mathcal{A}( X )$ on inputs $X$ the inequality

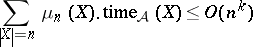has to hold for some fixed exponent $k$ (where $\mu _ { n } ( X )$ denotes the normalized restriction of $\mu$ as defined above). This would destroy the closure properties of polynomial time reductions. Instead, the relation

\begin{equation*} \sum _ { X } \mu ( X ) \frac { ( \operatorname { time } _ { \mathcal{A} } ( X ) ) ^ { 1 / k } } { | X | } < \infty \end{equation*}

is demanded for some number $k$, which is more robust against polynomial increase of running times and takes better into account the global probability distribution over the input space [a16].

To establish a notion corresponding to the worst-case class $\mathcal{P}$, one can consider distributional problems $( \mathcal{Q} , \mu )$ and require that there exists an algorithm solving $\mathcal{Q}$ in time polynomial on average with respect to this specific $\mu$ — this class is named $\mathcal{A} \mathcal{P}$, average-$\mathcal{P}$.

Alternatively, to allow a direct comparison to worst-case classes, one can restrict to computational problems $\mathcal{Q}$ and require that they can be solved polynomially on average for all distributions up to a certain complexity, for example for all polynomial-time computable distributions.

The hope that important worst-case intractable problems could be solved efficiently on average for polynomial-time computable distributions, in the case of $\cal N P$ called $\operatorname{Dist} \mathcal{NP}$, is questionable. There exists a surprisingly simple relation to worst-case complexity, namely the deterministic and non-deterministic exponential-time classes $\mathcal{DEXP}$ and $\cal N E X P$. If they are different — which is generally believed to be true, but a weaker condition than $\mathcal{P} \neq \mathcal{N} \mathcal{P}$ —, then $\operatorname{Dist} \mathcal{NP}$ is not contained in $\mathcal{A} \mathcal{P}$; in other words, there exist $\cal N P$-complete problems such that their distributional counterparts cannot be solved by a deterministic algorithm efficiently on the average.

An example of such a problem complete for the average case is the following so-called domino tiling problem [a16]. Given a set of dominos and a square partially covered with some of them, it requires one to fill the square completely. Every domino on each of its four sides carries a mark and in a legal tiling adjacent dominos must have identical marks at neighbouring sides. However, the number of problems complete for the average case that are known so far is significantly smaller than that for the worst case [a8].

To obtain a measure for average-case complexity that allows a better separation than simply polynomial or super-polynomial, these approaches have to be refined significantly. Given a time bound $T$, the class $\operatorname{AvDTime}( T )$ contains all distributional problems $( \mathcal{Q} , \mu )$ solvable by an algorithm $\mathcal{A}$ such that its average-case behaviour obeys the following bound for all $n$:

\begin{equation*} \sum _ { | X | \geq n } \mu ( X ) \frac { T ^ { - 1 } ( \operatorname { time } _ {\cal A } ( X ) ) } { | X | } \leq \sum _ { | X | \geq n } \mu ( X ), \end{equation*}

where $T ^ { - 1 }$ denotes a suitably defined inverse function of $T$. Given also a complexity bound $V$ on the distributions, the class $\operatorname{AvDTimeDis}( T , V )$ consists of all problems $\mathcal{Q}$ that for all distributions $\mu$ of complexity at most $V$ can be solved in $\mu$-average time $T$. This way, hierarchy results have been obtained for the average-case complexity similar to the worst case, showing that any slight increase of computation time or any slight decrease of the distribution complexity allows one to solve more algorithmic problems [a20], [a4]. By diagonalization arguments one can even exhibit problems with worst-case time complexity $T$ that cannot be solved in average time $T ^ { \prime }$ for any $T ^ { \prime } \leq o ( T )$.

For a detailed discussion of these concepts and further results, see [a8], [a1], [a23], [a20], [a24], [a25].

References

[a1]	S. Ben-David, B. Chor, O. Goldreich, M. Luby, "On the theory of average case complexity" J. Comput. Syst. Sci. , 44 (1992) pp. 193–219
[a2]	E. Bender, H. Wilf, "A theoretical analysis of backtracking in the graph coloring problem" J. Algorithms , 6 (1985) pp. 275–282
[a3]	K. Borgwardt, "The average number of pivot steps required by the simplex-method is polynomial" Z. Operat. Res. , 26 (1982) pp. 157–177
[a4]	J. Cai, A. Selman, "Fine separation of average time complexity classes" , Proc. 13 Symp. Theoret. Aspects of Computer Sci. , Lecture Notes in Compter Sci. , 1046 , Springer (1996) pp. 331–343
[a5]	P. Erdös, A. Renyi, "On the strength of connectedness of a random graph" Acta Math. Acad. Sci. Hungar. , 12 (1961) pp. 261–267
[a6]	P. Flajolet, B. Salvy, P. Zimmermann, "Automatic average-case analysis of algorithms" Theoret. Computer Sci. , 79 (1991) pp. 37–109
[a7]	Y. Gurevich, S. Shelah, "Expected computation time for Hamiltonian path problem" SIAM J. Comput. , 16 (1987) pp. 486–502
[a8]	Y. Gurevich, "Average case completeness" J. Comput. Syst. Sci. , 42 (1991) pp. 346–398
[a9]	A. Jakoby, R. Reischuk, C. Schindelhauer, "Circuit complexity: From the worst case to the average case" , Proc. 25th ACM Symp. Theory of Computing (1994) pp. 58–67
[a10]	A. Jakoby, R. Reischuk, C. Schindelhauer, "Malign distributions for average case circuit complexity" Inform. & Comput. , 150 (1999) pp. 187–208
[a11]	A. Jakoby, "Die Komplexität von Präfixfunktionen bezüglich ihres mittleren Zeitverhaltens" Diss. Univ. Lübeck, Shaker (1997)
[a12]	V. Klee, G. Minty, "How good is the simplex algorithm" , Inequalities , III , Acad. Press (1972) pp. 159–175
[a13]	A. Kamath, R. Motwani, K. Palem, P. Spirakis, "Tail bounds for occupancy and the satisfiability threshold" Random Struct. Algor. , 7 (1995) pp. 59–80
[a14]	J. Kratochvil, P. Savicky, Z. Tuza, "One more occurence of variables makes satisfiability jump from trivial to NP-complete" SIAM J. Comput. , 22 (1993) pp. 203–210
[a15]	M. Li, P. Vitanyi, "Average case complexity under the universal distribution equals worst case complexity" Inform. Proc. Lett. , 42 (1992) pp. 145–149
[a16]	L. Levin, "Average case complete problems" SIAM J. Comput. , 15 (1986) pp. 285–286
[a17]	D. Mitchel, B. Selman, H. Levesque, "Hard and easy distributions of SAT problems" , Proc. 10th Amer. Assoc. Artificial Intelligence , AAAI/MIT (1992) pp. 459–465
[a18]	P. Miltersen, "The complexity of malign measures" SIAM J. Comput. , 22 (1993) pp. 147–156
[a19]	P. Purdom, "A survey of average time analysis of satisfiability algorithms" J. Inform. Proces. , 13 (1990) pp. 449–455
[a20]	R. Reischuk, C. Schindelhauer, "An average complexity measure that yields tight hierarchies" Comput. Complexity , 6 (1996) pp. 133–173
[a21]	U. Rösler, "A limit theorem for quicksort" Theoret. Inform. Appl. , 25 (1991) pp. 85–100
[a22]	R. Sedgewick, "The analysis of quicksort programs" Acta Inform. , 7 (1977) pp. 327–355
[a23]	J. Wang, J. Belanger, "On average P vs. average NP" K. Ambos-Spies (ed.) S. Homer (ed.) U. Schning (ed.) , Complexity Theory Current Research , Cambridge Univ. Press (1993) pp. 47–68
[a24]	J. Wang, "Average-case computational complexity theory" A. Selman (ed.) L. Hemaspaandra (ed.) , Complexity Theory Retrospective , II , Springer (1997) pp. 295–328
[a25]	J. Wang, "Average-case intractable problems" D. Du (ed.) K. Ko (ed.) , Advances in Languages, Algorithms, and Complexity , Kluwer Acad. Publ. (1997) pp. 313–378