Eilenberg-Moore algebra
From Encyclopedia of Mathematics
Revision as of 16:45, 1 July 2020 by Maximilian Janisch (talk | contribs) (AUTOMATIC EDIT (latexlist): Replaced 10 formulas out of 12 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.)
Moore–Eilenberg algebra
Given a monad (or triple) $T$ in a category $\mathcal{C}$, a $T$-algebra is a pair $( A , \alpha )$, $\alpha : T A \rightarrow A$, $A \in \mathcal{C}$, such that the diagram
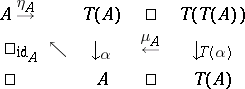 |
commutes. Such a $T$-algebra is also called an Eilenberg–Moore algebra. The forgetful functor from the category of Eilenberg–Moore algebras $\mathcal{C} ^ { T }$ to $\mathcal{C}$ has a left adjoint, exhibiting the monad $T$ as coming from a pair of adjoint functors (the Eilenberg–Moore construction).
See also Adjoint functor.
References
| [a1] | F. Borceux, "Handbook of categorical algebra: Categories and structures" , 2 , Cambridge Univ. Press (1994) pp. Chap. 4 |
How to Cite This Entry:
Eilenberg-Moore algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-Moore_algebra&oldid=50795
Eilenberg-Moore algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-Moore_algebra&oldid=50795
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article