B-Phi-structure
A structure on a vector bundle (or sphere bundle, etc.) that is a generalization of the concept of the structure group of a fibration.
Let  be a fibration and let
be a fibration and let  be an
be an  -dimensional vector bundle over a space
-dimensional vector bundle over a space  , classified by the mapping
, classified by the mapping  . Then the homotopy class lifting the mapping
. Then the homotopy class lifting the mapping  to a mapping in
to a mapping in 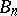 is called a
is called a  -structure on
-structure on 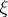 , i.e. it is an equivalence class of mappings
, i.e. it is an equivalence class of mappings 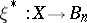 such that
such that  , where two mappings
, where two mappings 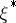 and
and  are said to be equivalent if they are fibrewise homotopic. No method of consistently defining
are said to be equivalent if they are fibrewise homotopic. No method of consistently defining 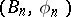 -structures for equivalent fibrations exists, because this consistency depends on the choice of the equivalence.
-structures for equivalent fibrations exists, because this consistency depends on the choice of the equivalence.
Let there be a sequence 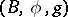 of fibrations
of fibrations 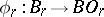 and mappings
and mappings 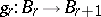 such that
such that 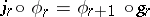 (
(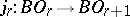 is the standard mapping). The family
is the standard mapping). The family 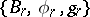 (and sometimes only
(and sometimes only 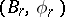 ) is called a structure series. An equivalence class of sequences of
) is called a structure series. An equivalence class of sequences of 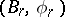 -structures on the normal bundle
-structures on the normal bundle 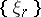 of a manifold
of a manifold  is called a
is called a 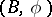 -structure on
-structure on 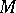 ; they coincide beginning from some sufficiently large
; they coincide beginning from some sufficiently large  . A manifold
. A manifold 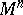 with a fixed
with a fixed  -structure on it is called a
-structure on it is called a 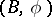 -manifold.
-manifold.
Instead of 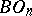 , a more general space
, a more general space  , classifying sphere bundles, can be considered and
, classifying sphere bundles, can be considered and  -structures can be introduced on them.
-structures can be introduced on them.
References
| [1] | R. Lashof, "Poincaré duality and cobordism" Trans. Amer. Math. Soc. , 109 (1963) pp. 257–277 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
Comments
Here
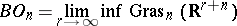 |
is the limit of the Grassmann manifolds of  -planes in
-planes in 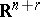 .
.
B-Phi-structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=B-Phi-structure&oldid=50466