Abstract wave equation

Consider the Cauchy problem for the wave equation

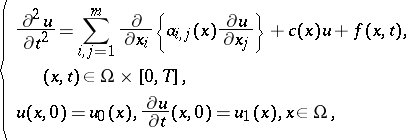with the Dirichlet boundary conditions or the Neumann boundary conditions , .

Here, 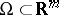is a bounded domain with smooth boundary , and are smooth real functions on such that 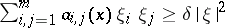for all 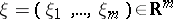, with some fixed 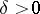; 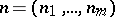is the unit outward normal vector to 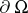. Also, 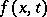, , 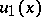are given functions. The function 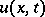is the unknown function.

One can state this problem in the abstract form

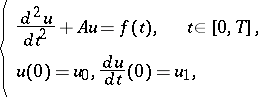(a1)

which is considered in the Hilbert space 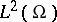. Here, 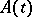is the self-adjoint operator of 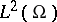determined from the symmetric sesquilinear form

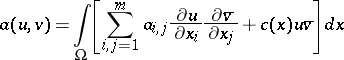(a2)

on the space 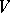, see [a1], where 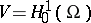(respectively 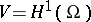) when the boundary conditions are Dirichlet (respectively, Neumann), by the relation 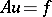if and only if 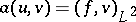for all 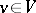. There are several ways to handle this abstract problem.

Let 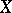be a Banach space. A strongly continuous function 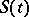of 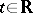with values in is called a cosine function if it satisfies 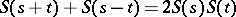, , 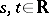and 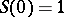. Its infinitesimal generator is defined by 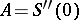, with 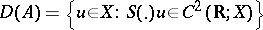. The theory of cosine functions, which is very similar to the theory of semi-groups, was originated by S. Kurera [a2] and was developed by H.O. Fattorini [a3] and others.

A necessary and sufficient condition for a closed linear operator to be the generator of a cosine family is known. The operator determined by (a2) is easily shown to generate a cosine function which provides a fundamental solution for (a1).

Suppose one sets 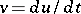in (a1). Then one obtains the equivalent problem

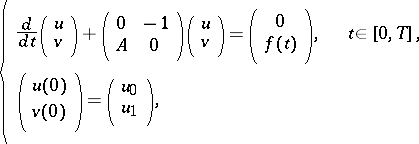which is considered in the product space . Since the equation is of first order, one can apply semi-group theory (see [a4], [a5]). Indeed, the operator

with its domain 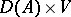is the negative generator of a 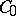semi-group. The theory of semi-groups of abstract evolution equations provides the existence of a unique solution 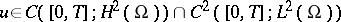of (a1) for 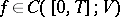and , .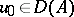

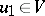This method is also available for a non-autonomous equation

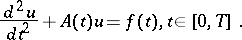(a3)

In the case of Neumann boundary conditions, the difficulty arises that the domain of

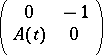may change with 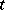. One way to avoid this is to introduce the extension 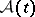of 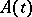defined by 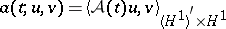for all . Since is a bounded operator from 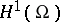into 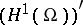, the operator

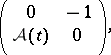acting in 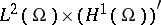, has constant domain.

Another way is to reduce (a3) to

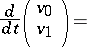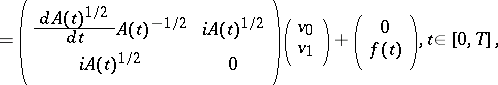by setting , , 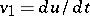under the assumption that 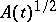is strongly differentiable with values in 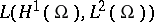. Obviously, the linear operator of the coefficient has constant domain 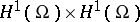. Differentiability of the square root 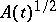was studied in [a6], [a7].

In order to consider in (a1) the case when 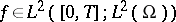, one has to use the Lions–Magenes variational formulation. In this, one is concerned with the solution of the problem

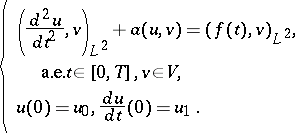The existence of a unique solution 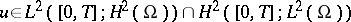has been proved if 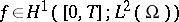and 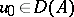, 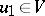; see [a8], Chap. 5.

This method is also available for a non-autonomous equation (a3).

The variational method enables one to take from a wide class, an advantage that is very useful in, e.g., the study of optimal control problems. On the other hand, the semi-group method provides regular solutions, which is often important in applications to non-linear problems. Using these approaches, many papers have been devoted to non-linear wave equations.

References

[a1]	J.-L. Lions, "Espaces d'interpolation et domaines de puissances fractionnaires d'opérateurs" J. Math. Soc. Japan , 14 (1962) pp. 233–241
[a2]	S. Kurepa, "A cosine functional equation in Hilbert spaces" Canad. J. Math. , 12 (1960) pp. 45–50
[a3]	H.O. Fattorini, "Ordinary differential equations in linear topological spaces II" J. Diff. Eq. , 6 (1969) pp. 50–70
[a4]	E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957)
[a5]	K. Yoshida, "Functional analysis" , Springer (1957)
[a6]	A. McIntosh, "Square roots of elliptic operators" J. Funct. Anal. , 61 (1985) pp. 307–327
[a7]	A. Yagi, "Applications of the purely imaginary powers of operators in Hilbert spaces" J. Funct. Anal. , 73 (1987) pp. 216–231
[a8]	J.-L. Lions, E. Magenes, "Problèmes aux limites non homogènes et applications" , 1–2 , Dunod (1968)