Specht module

Let and suppose is a (proper) partition of . This means that , where each and . If is maximal with , then one says that is a partition of into parts.

A 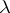-tableau (sometimes called a Young tableau associated with 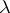) is an array consisting of the numbers 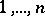listed in rows with exactly numbers occurring in the 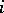th row, 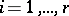. If, for instance, and 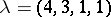, then the following arrays are examples of -tableaux:

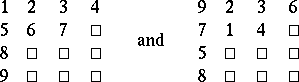One says that two 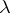-tableaux are equivalent if for each 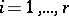the two sets of numbers in the 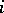th rows of the two arrays coincide. Clearly, the two 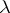-tableaux above are not equivalent. The equivalence classes with respect to this relation are called 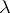-tabloids. If 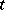is a -tableau, one usually denotes the 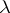-tabloid by 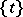. As examples, for 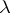as above one has

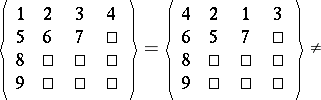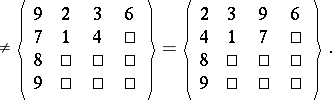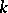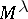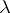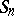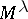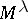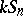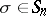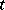Suppose is a field. Denote by the vector space over with basis equal to the set of -tabloids. Then the symmetric group on letters (cf. also Symmetric group) acts on (or, more precisely, is a -module) in a natural way. Indeed, if and is a 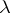-tableau, then 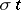is the 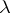-tableau obtained from 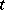by replacing each number 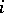by 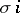. If one uses the usual cycle presentation of elements in , then, e.g., for 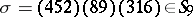one has

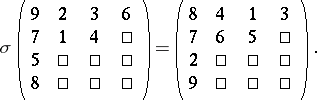This action clearly induces an action of on 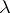-tabloids and this gives the desired module structure on .

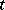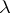If, again, is a -tableau, then one sets

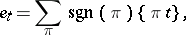where the sum runs over the 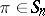that leave the set of numbers in each column in 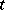stable. Here, 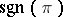is the sign of .

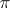The Specht module associated to 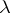is defined as the submodule

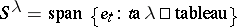of . Clearly, 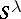is invariant under the action of 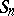. (In fact, 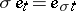for all and all 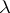-tableau .)

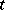Specht modules were introduced in 1935 by W. Specht [a5]. Their importance in the representation theory for symmetric groups (cf. also Representation of the symmetric groups) comes from the fact that when 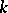contains 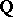, then each 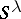is a simple -module. Moreover, the set

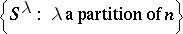is a full set of simple 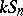-modules.

When the characteristic of 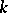is 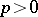, then the Specht modules are no longer always simple. However, they still play an important role in the classification of simple -modules. Namely, it turns out that when 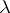is 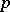-regular (i.e. no 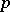parts of 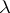are equal), then 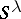has a unique simple quotient 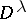and the set

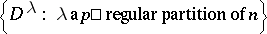constitutes a full set of simple 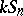-modules. It is a major open problem (1999) to determine the dimensions of these modules.

It is possible to give a (characteristic-free) natural basis for 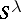. This is sometimes referred to as the Specht basis. In the notation above, it is given by

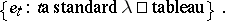Here, a 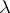-tableau 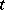is called standard if the numbers occurring in 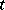are increasing along each row and down each column.

An immediate consequence is that the dimension of 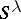equals the number of standard 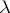-tableaux. For various formulas for this number (as well as many further properties of Specht modules) see [a2] and [a3].

The representation theory for symmetric groups is intimately related to the corresponding theory for general linear groups (Schur duality). Under this correspondence, Specht modules play the same role for 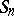as do the Weyl modules for 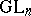, see e.g. [a1] and Weyl module. For a recent result exploring this correspondence in characteristic 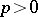, see [a4].

References

[a1]	J.A. Green, "Polynomial representations of 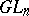" , Lecture Notes Math. , 830 , Springer (1980)
[a2]	G.D. James, "The representation theory of the symmetric groups" , Lecture Notes Math. , 682 , Springer (1978)
[a3]	G.D. James, A. Kerber, "The representation theory of the symmetric group" , Encycl. Math. Appl. , 16 , Addison-Wesley (1981)
[a4]	O. Mathieu, "On the dimension of some modular irreducible representations of the symmetric group" Lett. Math. Phys. , 38 (1996) pp. 23–32
[a5]	W. Specht, "Die irreduziblen Darstellungen der symmetrischen Gruppe" Math. Z. , 39 (1935) pp. 696–711