Bazilevich functions
Let 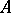 be the class of functions
be the class of functions 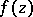 that are analytic in the open unit disc
that are analytic in the open unit disc 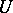 with
with 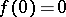 and
and 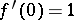 (cf. also Analytic function). Let
(cf. also Analytic function). Let 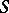 denote the subclass of
denote the subclass of 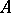 consisting of all univalent functions in
consisting of all univalent functions in 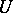 (cf. also Univalent function). Further, let
(cf. also Univalent function). Further, let 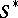 denote the subclass of
denote the subclass of 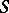 consisting of functions that are starlike with respect to the origin (cf. also Univalent function).
consisting of functions that are starlike with respect to the origin (cf. also Univalent function).
The Kufarev differential equation
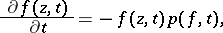 | (a1) |
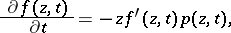 | (a2) |
where 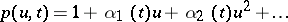 is a function regular in
is a function regular in 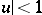 , having positive real part and being piecewise continuous with respect to a parameter
, having positive real part and being piecewise continuous with respect to a parameter 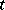 , plays an important part in the theory of univalent functions. This differential equation can be generalized as the corresponding Loewner differential equation
, plays an important part in the theory of univalent functions. This differential equation can be generalized as the corresponding Loewner differential equation
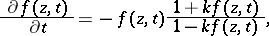 | (a3) |
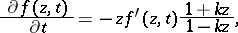 | (a4) |
where 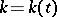 is a continuous complex-valued function with
is a continuous complex-valued function with 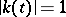 (
(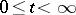 ).
).
Letting 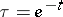 (
(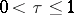 ), (a1) can be written in the form
), (a1) can be written in the form
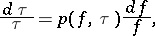 | (a5) |
where 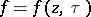 ,
, 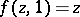 , and
, and 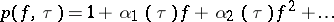 is a function regular in
is a function regular in 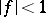 with
with 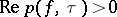 . Introducing a real parameter
. Introducing a real parameter  , one sets
, one sets
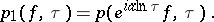 |
Further, making the change 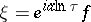 , one obtains
, one obtains
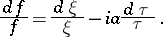 |
Making the changes 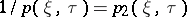 with
with 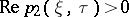 and
and
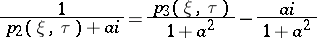 |
with 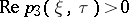 , one obtains
, one obtains
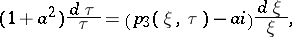 | (a6) |
which is the generalization of (a5).
Writing
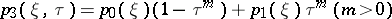 |
with
 |
and
 |
(a6) gives the Bernoulli equation
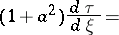 | (a7) |
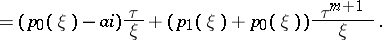 |
If one takes
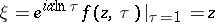 |
in (a7), one obtains the integral
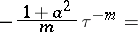 | (a8) |
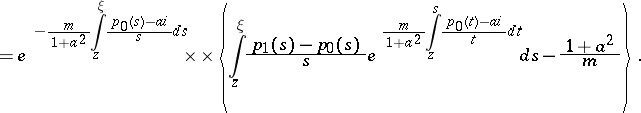 |
Using
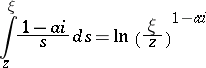 |
and  , one sees that
, one sees that 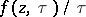 is uniformly convergent to a certain function
is uniformly convergent to a certain function 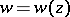 of the class
of the class 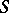 . This implies that
. This implies that
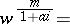 | (a9) |
 |
Noting that (a9) implies
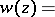 | (a10) |
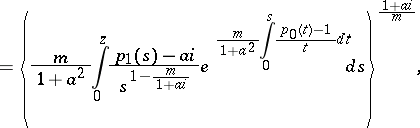 |
I.E. Bazilevich [a1] proved that the function 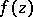 given by
given by
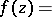 | (a11) |
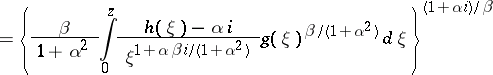 |
belongs to the class 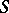 , where
, where
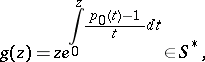 |
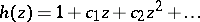 is regular in
is regular in 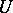 with
with 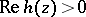 ,
, 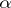 is any real number, and
is any real number, and 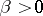 .
.
If one sets 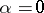 in (a11), then
in (a11), then
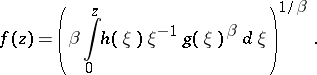 | (a12) |
Since 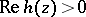 in
in 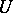 , the function
, the function 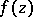 given by (a12) satisfies
given by (a12) satisfies
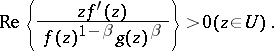 | (a13) |
Therefore, the function 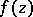 satisfying (a13) with
satisfying (a13) with 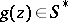 is called a Bazilevich function of type
is called a Bazilevich function of type 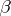 .
.
Denote by 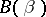 the class of functions
the class of functions 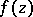 that are Bazilevich of type
that are Bazilevich of type 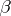 in
in 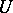 .
.
1) If 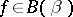 with
with 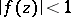 in
in 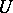 , then
, then
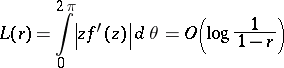 |
as  (see [a3]).
(see [a3]).
2) Let 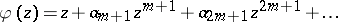 be analytic in
be analytic in 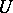 . Then
. Then 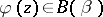 if and only if
if and only if 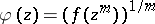 with
with 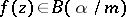 (see [a7]).
(see [a7]).
3) T. Sheil-Small [a12] has introduced the class of Bazilevich functions of type 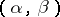 , given by
, given by
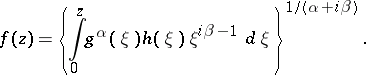 |
4) If 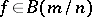 , then
, then 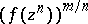 is a close-to-convex
is a close-to-convex 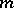 -valent function, where
-valent function, where 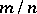 is a rational number (see [a9]).
is a rational number (see [a9]).
For other properties of Bazilevich functions, see [a4], [a8], [a10], [a2], [a6], [a11], and [a5].
References
| [a1] | I.E. Bazilevich, "On a class of integrability by quadratures of the equation of Loewner–Kufarev" Mat. Sb. , 37 (1955) pp. 471–476 |
| [a2] | R. Singh, "On Bazilevič functions" Proc. Amer. Math. Soc. , 38 (1973) pp. 261–271 |
| [a3] | D.K. Thomas, "On Bazilevič functions" Trans. Amer. Math. Soc. , 132 (1968) pp. 353–361 |
| [a4] | J. Zamorski, "On Bazilevič schlicht functions" Ann. Polon. Math. , 12 (1962) pp. 83–90 |
| [a5] | P.L. Duren, "Univalent functions" , Grundl. Math. Wissenschaft. , 259 , Springer (1983) |
| [a6] | P.J. Eenigenburg, S.S. Miller, P.T. Mocanu, M.O. Reade, "On a subclass of Bazilevič functions" Proc. Amer. Math. Soc. , 45 (1974) pp. 88–92 |
| [a7] | F.R. Keogh, S.S. Miller, "On the coefficients of Bazilevič functions" Proc. Amer. Math. Soc. , 30 (1971) pp. 492–496 |
| [a8] | S.S. Miller, "The Hardy class of a Bazilevič function and its derivative" Proc. Amer. Math. Soc. , 30 (1971) pp. 125–132 |
| [a9] | P.T. Mocanu, M.O. Reade, E.J. Zlotkiewicz, "On Bazilevič functions" Proc. Amer. Math. Soc. , 39 (1973) pp. 173–174 |
| [a10] | M. Nunokawa, "On the Bazilevič analytic functions" Sci. Rep. Fac. Edu. Gunma Univ. , 21 (1972) pp. 9–13 |
| [a11] | Ch. Pommerenke, "Univalent functions" , Vandenhoeck&Ruprecht (1975) |
| [a12] | T. Sheil-Small, "On Bazilevič functions" Quart. J. Math. , 23 (1972) pp. 135–142 |
Bazilevich functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bazilevich_functions&oldid=50402