Dunford integral
From Encyclopedia of Mathematics
An integral playing a key role in the Riesz–Dunford functional calculus for Banach spaces (cf. Functional calculus.) In this calculus, for a fixed bounded linear operator 
on a Banach space 
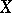, all functions 
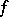holomorphic on a neighbourhood 
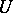of the spectrum 
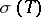of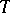 
(cf. also Spectrum of an operator) are turned into a bounded linear operator 
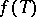on 
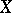by
 |
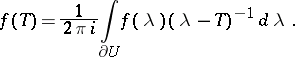This integral is called the Dunford integral. It is assumed here that the boundary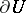 
of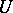 
consists of a finite number of rectifiable Jordan curves (cf. also Jordan curve), oriented in positive sense.
For suitably chosen domains of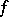 
and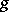 
, the following rules of operational calculus hold:
 |
 |
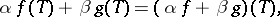Also,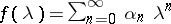 
on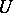 
implies 
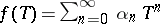in the operator norm. If 
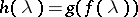, then 
.
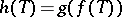The Dunford integral can be considered as a Bochner integral.
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators" , 1 , Interscience (1958) |
| [a2] | K. Yosida, "Functional analysis" , Springer (1980) |
How to Cite This Entry:
Dunford integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dunford_integral&oldid=50341
Dunford integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dunford_integral&oldid=50341
This article was adapted from an original article by J. de Graaf (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article