Bohnenblust theorem
Consider the space 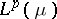 ,
, 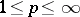 , and a measure space
, and a measure space 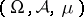 . Since the norm
. Since the norm 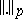 is
is 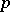 -additive, it is easily seen that the following condition is satisfied: For all
-additive, it is easily seen that the following condition is satisfied: For all 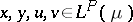 satisfying
satisfying 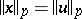 ,
, 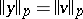 ,
, 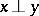 and
and 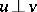 (in the sense of disjoint support), one has
(in the sense of disjoint support), one has 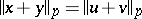 .
.
In [a2] H.F. Bohnenblust showed that the spaces 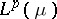 are the only Banach lattices (cf. also Banach lattice) possessing this property; more precisely, he proved the following theorem, now known as the Bohnenblust theorem: Let
are the only Banach lattices (cf. also Banach lattice) possessing this property; more precisely, he proved the following theorem, now known as the Bohnenblust theorem: Let  be a Banach lattice of dimension
be a Banach lattice of dimension 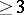 satisfying
satisfying 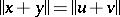 for all
for all 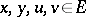 such that
such that 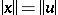 ,
, 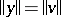 ,
, 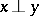 , and
, and 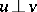 . Then there exists a
. Then there exists a 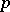 ,
, 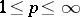 , such that the norm on
, such that the norm on  is
is 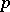 -additive.
-additive.
Here, for 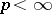 , a norm is said to be
, a norm is said to be 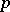 -additive if
-additive if 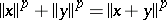 for all
for all 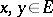 with
with 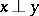 ; a norm is said to be
; a norm is said to be 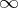 -additive, or, equivalently,
-additive, or, equivalently, 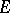 is said to be an
is said to be an 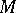 -space, if
-space, if 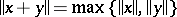 for all
for all 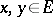 with
with  .
.
It should be noted that when 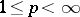 , every Banach lattice with a
, every Banach lattice with a  -additive norm is isometrically isomorphic to
-additive norm is isometrically isomorphic to 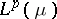 , with
, with 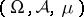 a suitable measure space. This representation theorem is essentially due to S. Kakutani [a3], who considered the case
a suitable measure space. This representation theorem is essentially due to S. Kakutani [a3], who considered the case 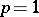 ; the proof of the more general result follows almost the same lines. For
; the proof of the more general result follows almost the same lines. For 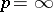 the situation is not so clear: there exist many
the situation is not so clear: there exist many 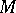 -spaces that are not isomorphic to any concrete
-spaces that are not isomorphic to any concrete 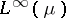 -space, for instance
-space, for instance 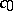 .
.
In the proof of his theorem, H.F. Bohnenblust introduced an interesting and tricky method to construct the 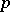 such that the norm is
such that the norm is 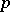 -additive. A similar method was used later by M. Zippin [a5] to characterize
-additive. A similar method was used later by M. Zippin [a5] to characterize 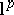 -spaces in terms of bases. Since the proof given by Bohnenblust is interesting in itself, the main ideas are sketched below.
-spaces in terms of bases. Since the proof given by Bohnenblust is interesting in itself, the main ideas are sketched below.
By hypothesis, there exists a function 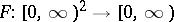 defined by
defined by
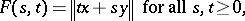 |
whenever  and
and 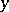 are disjoint vectors of norm one. It can easily be verified that the function
are disjoint vectors of norm one. It can easily be verified that the function 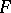 has the following properties:
has the following properties:
1) 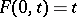 ;
;
ii) 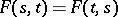 ;
;
iii) 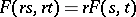 ;
;
iv) 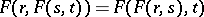 ;
;
v) 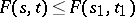 if
if 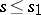 ,
,  . The only non-trivial inclusion iv) follows from
. The only non-trivial inclusion iv) follows from
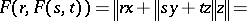 |
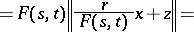 |
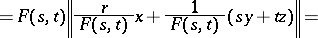 |
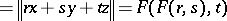 |
for all disjoint 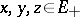 of norm one and
of norm one and 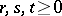 with
with 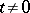 .
.
One defines 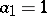 and
and 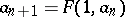 for all
for all 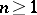 . Property v) implies that the sequence
. Property v) implies that the sequence 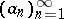 is increasing. By induction one obtains
is increasing. By induction one obtains 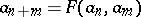 and
and 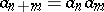 . If
. If 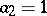 , then properties i)–v) easily imply
, then properties i)–v) easily imply 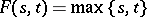 for all
for all 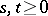 . Hence,
. Hence, 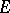 is an
is an 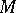 -space.
-space.
Assume now that 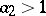 and let
and let 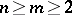 . For all
. For all 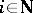 there exists a
there exists a 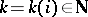 such that
such that 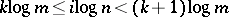 . Since
. Since 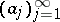 is an increasing sequence, one concludes from
is an increasing sequence, one concludes from 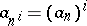 that
that  or, equivalently, that
or, equivalently, that 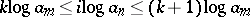 . This yields
. This yields
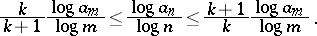 |
Letting 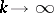 ,
,
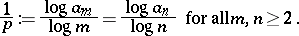 |
It is clear that 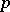 does not depend on the special choice of
does not depend on the special choice of 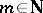 . Moreover,
. Moreover, 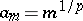 for all
for all 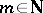 . Since
. Since 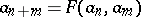 , it follows that
, it follows that 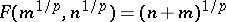 for all
for all 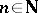 . Consequently,
. Consequently,
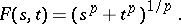 |
From 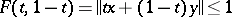 for all
for all 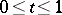 it follows that
it follows that 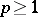 . This completes the proof.
. This completes the proof.
Bohnenblust's theorem has some interesting consequences. For instance, T. Ando [a1] used it to prove that a Banach lattice 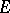 is isometrically isomorphic to
is isometrically isomorphic to 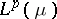 for some measure space
for some measure space 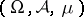 , or to some
, or to some 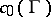 , if and only if every closed sublattice of
, if and only if every closed sublattice of 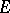 is the range of a positive contractive projection.
is the range of a positive contractive projection.
References
| [a1] | T. Ando, "Banachverbände und positive Projektionen" Math. Z. , 109 (1969) pp. 121–130 |
| [a2] | H.F. Bohnenblust, "An axiomatic characterization of 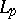 -spaces" Duke Math. J. , 6 (1940) pp. 627–640 -spaces" Duke Math. J. , 6 (1940) pp. 627–640 |
| [a3] | S. Kakutani, "Concrete representation of abstract 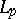 -spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 -spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 |
| [a4] | P. Meyer-Nieberg, "Banach lattices" , Springer (1991) |
| [a5] | M. Zippin, "On perfectly homogeneous bases in Banach spaces" Israel J. Math. , 4 A (1966) pp. 265–272 |
Bohnenblust theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohnenblust_theorem&oldid=50317