X-inner automorphism
 -inner automorphisms were introduced by V.K. Kharchenko in [a2] and [a3] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also Prime ring; Rings and algebras). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let
-inner automorphisms were introduced by V.K. Kharchenko in [a2] and [a3] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also Prime ring; Rings and algebras). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let 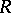 be a prime ring (with
be a prime ring (with 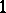 ) and let
) and let 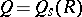 denote its symmetric Martindale ring of quotients. Then any automorphism
denote its symmetric Martindale ring of quotients. Then any automorphism 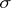 of
of 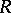 extends uniquely to an automorphism
extends uniquely to an automorphism  of
of 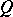 , and one says that
, and one says that 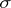 is
is  -inner if
-inner if 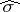 is inner on
is inner on 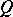 (cf. also Inner automorphism). It is easy to see that
(cf. also Inner automorphism). It is easy to see that 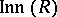 , the set of all
, the set of all 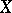 -inner automorphisms of
-inner automorphisms of 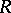 , is a normal subgroup of
, is a normal subgroup of 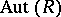 .
.
 -inner automorphisms control the generalized linear identities of
-inner automorphisms control the generalized linear identities of 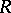 , namely those linear identities which involve automorphisms. For example, it is shown in [a2] that if
, namely those linear identities which involve automorphisms. For example, it is shown in [a2] that if  and if
and if 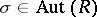 with
with 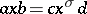 for all
for all 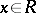 , then there exists a unit
, then there exists a unit  with
with 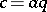 ,
,  and
and 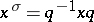 for all
for all 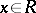 . In particular,
. In particular, 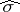 is the inner automorphism of
is the inner automorphism of 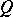 induced by
induced by 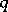 and consequently
and consequently 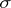 is
is 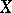 -inner. Of course,
-inner. Of course, 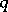 is determined by
is determined by 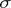 up to multiplication by a non-zero element of the extended centroid
up to multiplication by a non-zero element of the extended centroid 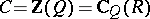 .
.
Now, let 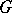 be a group of automorphisms of
be a group of automorphisms of 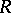 and let
and let  , so that
, so that 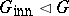 . If
. If  denotes the linear span of all units
denotes the linear span of all units 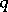 in
in 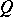 such that conjugation by
such that conjugation by 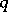 belongs to
belongs to 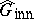 , then
, then  is a
is a 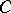 -subalgebra of
-subalgebra of 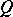 , called the algebra of the group (cf. also Group algebra). One says that
, called the algebra of the group (cf. also Group algebra). One says that 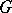 is an
is an 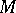 -group (Maschke group) if
-group (Maschke group) if 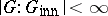 and if
and if 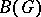 is a finite-dimensional semi-simple
is a finite-dimensional semi-simple 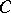 -algebra. Furthermore,
-algebra. Furthermore, 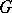 is an
is an 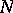 -group (Noether group) if
-group (Noether group) if 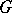 is an
is an 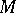 -group and if conjugation by every unit of
-group and if conjugation by every unit of 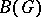 induces an automorphism of
induces an automorphism of 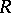 contained in
contained in 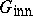 . The Galois theory, as developed in [a3] and [a14], involves the action of
. The Galois theory, as developed in [a3] and [a14], involves the action of 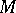 -groups and
-groups and 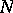 -groups on prime rings.
-groups on prime rings.
Note that if 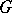 is an
is an 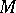 -group and if
-group and if 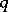 is a unit of
is a unit of 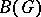 , then conjugation by
, then conjugation by 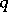 need not stabilize
need not stabilize 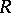 . Thus, it is not always possible to embed an
. Thus, it is not always possible to embed an 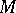 -group into an
-group into an 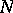 -group. One can avoid this difficulty by extending the definition of "automorphism of R" to include those (real) automorphisms
-group. One can avoid this difficulty by extending the definition of "automorphism of R" to include those (real) automorphisms  of
of 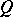 such that
such that 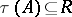 for some
for some  .
.
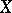 -inner automorphisms also appear prominently in the study of cross products. For example, it is proved in [a1] that if
-inner automorphisms also appear prominently in the study of cross products. For example, it is proved in [a1] that if  is a cross product over the prime ring
is a cross product over the prime ring 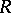 , then
, then  embeds naturally into
embeds naturally into 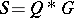 and that
and that 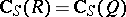 is a twisted group algebra
is a twisted group algebra 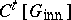 with
with 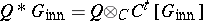 . Furthermore, it is shown in [a9] that every non-zero ideal of
. Furthermore, it is shown in [a9] that every non-zero ideal of 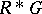 meets
meets 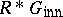 non-trivially, and in [a11] that
non-trivially, and in [a11] that 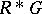 is prime (or semi-prime) if and only if
is prime (or semi-prime) if and only if 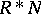 is
is  -prime (or
-prime (or 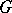 -semi-prime) for all finite normal subgroups
-semi-prime) for all finite normal subgroups 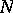 of
of 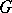 contained in
contained in 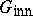 . The above-mentioned structure of
. The above-mentioned structure of 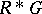 is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
There are numerous computations of 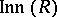 in the literature. To start with, it is shown in [a4] that if
in the literature. To start with, it is shown in [a4] that if 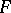 is a non-commutative free algebra, then
is a non-commutative free algebra, then 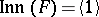 . More general free products are studied in [a7] and [a8]. Next, [a10] effectively handles graded domains like enveloping algebras of Lie algebras, and [a15] considers arbitrary enveloping algebra smash products. Finally, [a12] and [a13] study certain group algebras and show that for any group
. More general free products are studied in [a7] and [a8]. Next, [a10] effectively handles graded domains like enveloping algebras of Lie algebras, and [a15] considers arbitrary enveloping algebra smash products. Finally, [a12] and [a13] study certain group algebras and show that for any group 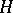 there exists a domain
there exists a domain 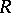 with
with 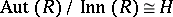 .
.
Now suppose that 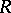 is a semi-prime ring and again let
is a semi-prime ring and again let 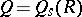 denote its symmetric Martindale ring of quotients. If
denote its symmetric Martindale ring of quotients. If 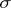 is an arbitrary automorphism of
is an arbitrary automorphism of 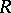 , write
, write 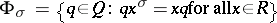 . Then, following [a2], one says that
. Then, following [a2], one says that 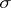 is
is 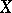 -inner if
-inner if 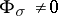 . Of course,
. Of course, 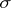 is
is 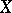 -outer when
-outer when 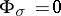 . Note that, in the case of semi-prime rings,
. Note that, in the case of semi-prime rings, 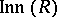 need not be a subgroup of
need not be a subgroup of 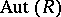 . Nevertheless, a good deal of structure still exists. For example, [a3] proves the key fact that
. Nevertheless, a good deal of structure still exists. For example, [a3] proves the key fact that 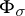 is always a cyclic
is always a cyclic  -module.
-module.
References
| [a1] | J.W. Fisher, S. Montgomery, "Semiprime skew group rings" J. Algebra , 52 (1978) pp. 241–247 |
| [a2] | V.K. Kharchenko, "Generalized identities with automorphisms" Algebra and Logic , 14 (1976) pp. 132–148 Algebra i Logika , 14 (1975) pp. 215–237 |
| [a3] | V.K. Kharchenko, "Galois theory of semiprime rings" Algebra and Logic , 16 (1978) pp. 208–258 Algebra i Logika , 16 (1977) pp. 313–363 |
| [a4] | V.K. Kharchenko, "Algebras of invariants of free algebras" Algebra and Logic , 17 (1979) pp. 316–321 Algebra i Logika , 17 (1978) pp. 478–487 |
| [a5] | M. Lorenz, D.S. Passman, "Prime ideals in crossed products of finite groups" Israel J. Math. , 33 (1979) pp. 89–132 |
| [a6] | M. Lorenz, D.S. Passman, "Prime ideals in group algebras of polycyclic-by-finite groups" Proc. London Math. Soc. , 43 (1981) pp. 520–543 |
| [a7] | W.S. Martindale III, "The normal closure of the coproduct of rings over a division ring" Trans. Amer. Math. Soc. , 293 (1986) pp. 303–317 |
| [a8] | W.S. Martindale III, S. Montgomery, "The normal closure of coproducts of domains" J. Algebra , 82 (1983) pp. 1–17 |
| [a9] | S. Montgomery, "Outer automorphisms of semi-prime rings" J. London Math. Soc. , 18 : 2 (1978) pp. 209–220 |
| [a10] | S. Montgomery, "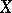 -inner automorphisms of filtered algebras" Proc. Amer. Math. Soc. , 83 (1981) pp. 263–268 -inner automorphisms of filtered algebras" Proc. Amer. Math. Soc. , 83 (1981) pp. 263–268 |
| [a11] | S. Montgomery, D.S. Passman, "Crossed products over prime rings" Israel J. Math. , 31 (1978) pp. 224–256 |
| [a12] | S. Montgomery, D.S. Passman, "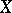 -Inner automorphisms of group rings" Houston J. Math. , 7 (1981) pp. 395–402 -Inner automorphisms of group rings" Houston J. Math. , 7 (1981) pp. 395–402 |
| [a13] | S. Montgomery, D.S. Passman, "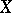 -Inner automorphisms of group rings II" Houston J. Math. , 8 (1982) pp. 537–544 -Inner automorphisms of group rings II" Houston J. Math. , 8 (1982) pp. 537–544 |
| [a14] | S. Montgomery, D.S. Passman, "Galois theory of prime rings" J. Pure Appl. Algebra , 31 (1984) pp. 139–184 |
| [a15] | J. Osterburg, D.S. Passman, " -inner automorphisms of enveloping rings" J. Algebra , 130 (1990) pp. 412–434 -inner automorphisms of enveloping rings" J. Algebra , 130 (1990) pp. 412–434 |
X-inner automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=X-inner_automorphism&oldid=50067