Matrix variate elliptically contoured distribution
The class of matrix variate elliptically contoured distributions can be defined in many ways. Here the definition of A.K. Gupta and T. Varga [a4] is given.
A random matrix 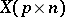 (see Matrix variate distribution) is said to have a matrix variate elliptically contoured distribution if its characteristic function has the form
(see Matrix variate distribution) is said to have a matrix variate elliptically contoured distribution if its characteristic function has the form 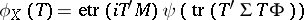 with
with 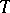 a
a  -matrix,
-matrix,  a
a 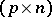 -matrix,
-matrix, 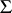 a
a 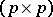 -matrix,
-matrix, 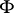 a
a  -matrix,
-matrix, 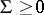 ,
, 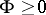 and
and  . This distribution is denoted by
. This distribution is denoted by 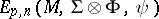 . If the distribution of
. If the distribution of 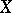 is absolutely continuous (cf. also Absolute continuity), then its probability density function (cf. also Density of a probability distribution) has the form
is absolutely continuous (cf. also Absolute continuity), then its probability density function (cf. also Density of a probability distribution) has the form
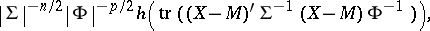 |
where 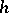 and
and 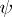 determine each other.
determine each other.
An important subclass of the class of matrix variate elliptically contoured distributions is the class of matrix variate normal distributions. A matrix variate elliptically contoured distribution has many properties which are similar to the normal distribution. For example, linear functions of a random matrix with a matrix variate elliptically contoured distribution also have elliptically contoured distributions. That is, if 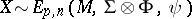 , then for given constant matrices
, then for given constant matrices 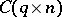 ,
, 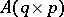 ,
, 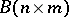 ,
,  .
.
If 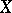 ,
, 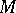 and
and 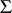 are partitioned as
are partitioned as
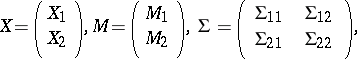 |
where 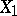 is a
is a 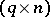 -matrix,
-matrix, 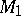 is a
is a 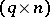 -matrix and
-matrix and 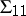 is a
is a  -matrix,
-matrix, 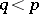 , then
, then  . However, if
. However, if 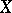 ,
, 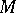 and
and 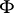 are partitioned as
are partitioned as
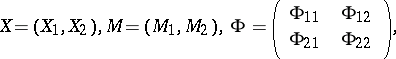 |
where 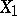 is a
is a 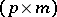 -matrix,
-matrix, 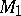 is a
is a 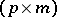 -matrix, and
-matrix, and 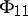 is an
is an 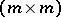 -matrix,
-matrix, 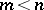 , then
, then 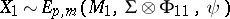 .
.
Here, if the expectations exist, then 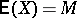 and
and 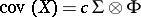 , where
, where 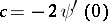 . An important tool in the study of matrix variate elliptically contoured distributions is the stochastic representation of
. An important tool in the study of matrix variate elliptically contoured distributions is the stochastic representation of 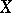 :
:
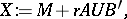 |
where 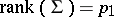 ,
, 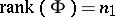 ,
, 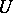 is a
is a 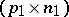 -matrix and
-matrix and 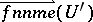 is uniformly distributed on the unit sphere in
is uniformly distributed on the unit sphere in 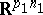 ,
,  is a non-negative random variable,
is a non-negative random variable,  and
and 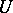 are independent,
are independent, 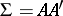 , and
, and  . Moreover,
. Moreover,
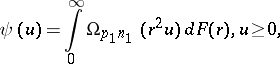 |
where 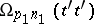 ,
, 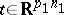 denotes the characteristic function of
denotes the characteristic function of 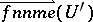 , and
, and  denotes the distribution function of
denotes the distribution function of  .
.
References
| [a1] | K.T. Fang, Y.T. Zhang, "Generalized multivariate analysis" , Springer (1990) |
| [a2] | K.T. Fang, T.W. Anderson, "Statistical inference in elliptically contoured and related distributions" , Allerton Press (1990) |
| [a3] | A.K. Gupta, T. Varga, "Rank of a quadratic form in an elliptically contoured matrix random variable" Statist. Probab. Lett. , 12 (1991) pp. 131–134 |
| [a4] | A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993) |
| [a5] | A.K. Gupta, T. Varga, "Some applications of the stochastic representation of elliptically contoured distribution" Random Oper. and Stoch. Eqs. , 2 (1994) pp. 1–11 |
| [a6] | A.K. Gupta, T. Varga, "A new class of matrix variate elliptically contoured distributions" J. Italian Statist. Soc. , 3 (1994) pp. 255–270 |
| [a7] | A.K. Gupta, T. Varga, "Moments and other expected values for matrix variate elliptically contoured distributions" Statistica , 54 (1994) pp. 361–373 |
| [a8] | A.K. Gupta, T. Varga, "Normal mixture representation of matrix variate elliptically contoured distributions" Sankhyā Ser. A , 57 (1995) pp. 68–78 |
| [a9] | A.K. Gupta, T. Varga, "Some inference problems for matrix variate elliptically contoured distributions" Statistics , 26 (1995) pp. 219–229 |
| [a10] | A.K. Gupta, T. Varga, "Characterization of matrix variate elliptically contoured distributions" , Adv. Theory and Practice of Statistics: A Volume in Honor of Samuel Kotz , Wiley (1997) pp. 455–467 |
Matrix variate elliptically contoured distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_variate_elliptically_contoured_distribution&oldid=50045