Sperner property
Let 
be a finite partially ordered set (abbreviated: poset) which possesses a rank function 
, i.e. a function 
such that 
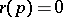for some minimal element 
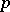of 
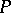and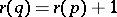 
whenever 
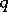covers 
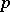, i.e. 
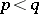and there is no element between 
and 
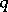. Let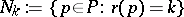 
be its 
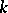th level and let 
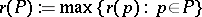be the rank of 
.
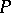An anti-chain or Sperner family in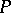 
is a subset of pairwise incomparable elements of 
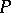. Obviously, each level is an anti-chain. The width of a partially ordered set 
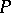(Dilworth number or Sperner number) is the maximum size 
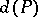of an anti-chain of 
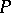. The poset 
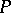is said to have the Sperner property if 
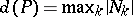. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also Sperner theorem).
More generally, a 
-family, 
, is a subset of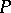 
containing no chain of 
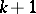elements in 
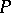, and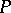 
has the strong Sperner property if for each 
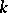the largest size of a 
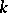-family in 
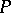equals the largest size of a union of 
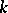levels. There exist several classes of posets having the strong Sperner property:
LYM posets, i.e. posets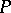 
satisfying the LYM inequality (cf. also Sperner theorem)
 |
for every anti-cha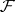in 
in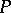 
or, equivalently,
 |
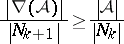for all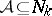 
, 
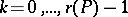, where 
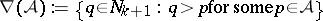. This equivalent property is called the normalized matching property of 
.
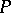Symmetric chain orders, i.e. ranked posets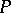 
which can be decomposed into chains of the form 
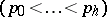where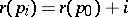 
, 
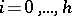, and 
.
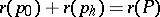Peck posets, i.e. ranked posets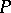 
such that 
for all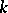 
and there is a linear operator 
on the vector space having the basis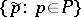 
with the following properties:
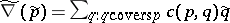with some numbers 
,
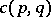the subspace generated by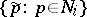 
is mapped via 
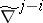to a subspace of dimension 
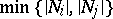for all 
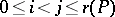. If 
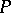and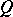 
are posets from one class, then also the direct product 
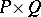(ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: 
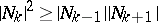for all 
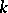(so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.
Every LYM poset with the symmetry and unimodality property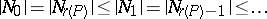 
is a symmetric chain order and every symmetric chain order is a Peck poset.
Standard examples of posets belonging to all these three classes are the lattice of subsets of a finite set, ordered by inclusion (the Boolean lattice), the lattice of divisors of a natural number, ordered by divisibility, the lattice of all subspaces of an 
-dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an 
-dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if 
is sufficiently large.
Details can be found in [a1].
References
| [a1] | K. Engel, "Sperner theory" , Cambridge Univ. Press (1997) |
Sperner property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sperner_property&oldid=50032