Toeplitz operator
Together with the class of Hankel operators (cf. also Hankel operator), the class of Toeplitz operators is one of the most important classes of operators on Hardy spaces. A Toeplitz operator can be defined as an operator on 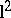 with matrix of the form
with matrix of the form 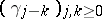 . The following boundedness criterion was obtained by P.R. Halmos (see [a1], [a5]): Let
. The following boundedness criterion was obtained by P.R. Halmos (see [a1], [a5]): Let 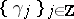 be a sequence of complex numbers and let
be a sequence of complex numbers and let 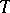 be the operator on
be the operator on 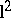 with matrix
with matrix 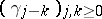 . Then
. Then 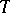 is bounded if and only if there exists a function
is bounded if and only if there exists a function 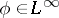 on the unit circle
on the unit circle 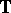 such that
such that
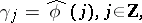 |
where the 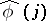 ,
, 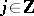 , are the Fourier coefficients of
, are the Fourier coefficients of 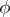 (cf. also Fourier series).
(cf. also Fourier series).
This theorem allows one to consider the following realization of Toeplitz operators on the Hardy class 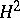 (cf. also Hardy classes). Let
(cf. also Hardy classes). Let 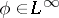 . One defines the Toeplitz operator
. One defines the Toeplitz operator 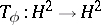 by
by 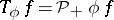 , where
, where 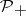 is the orthogonal projection onto
is the orthogonal projection onto 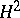 . The function
. The function 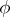 is called the symbol of
is called the symbol of 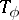 .
.
Toeplitz operators are important in many applications (prediction theory, boundary-value problems for analytic functions, singular integral equations). Toeplitz operators are unitarily equivalent to Wiener–Hopf operators (cf. also Wiener–Hopf operator). For a function 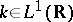 one can define the Wiener–Hopf operator
one can define the Wiener–Hopf operator 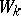 on
on 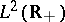 by
by
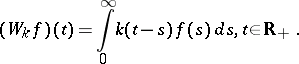 |
Then 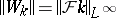 , where
, where 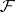 is the Fourier transform. The definition of Wiener–Hopf operators can be extended to the case when
is the Fourier transform. The definition of Wiener–Hopf operators can be extended to the case when 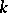 is a tempered distribution whose Fourier transform is in
is a tempered distribution whose Fourier transform is in 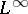 . In this case,
. In this case, 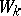 is unitarily equivalent to the Toeplitz operator
is unitarily equivalent to the Toeplitz operator 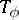 , where
, where 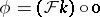 and
and  is a conformal mapping from the unit disc onto the upper half-plane.
is a conformal mapping from the unit disc onto the upper half-plane.
The mapping 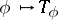 defined on
defined on 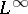 is linear but not multiplicative. In fact,
is linear but not multiplicative. In fact, 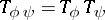 if and only if
if and only if 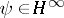 or
or 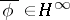 (Halmos' theorem, see [a1]). It is easy to see that
(Halmos' theorem, see [a1]). It is easy to see that 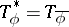 .
.
It is important in applications to be able to solve Toeplitz equations 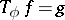 . Therefore one of the most important problems in the study of Toeplitz operators is to describe the spectrum
. Therefore one of the most important problems in the study of Toeplitz operators is to describe the spectrum 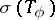 and the essential spectrum
and the essential spectrum 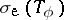 (cf. also Spectrum of an operator).
(cf. also Spectrum of an operator).
Unlike the case of arbitrary operators, a Toeplitz operator 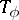 is invertible if and only if it is Fredholm and its index
is invertible if and only if it is Fredholm and its index 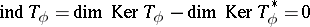 . This is a consequence of the following lemma, which is due to L.A.. Coburn ([a1]): If
. This is a consequence of the following lemma, which is due to L.A.. Coburn ([a1]): If 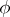 is a non-zero function in
is a non-zero function in 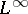 , then either
, then either 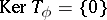 or
or 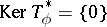 .
.
Hence,
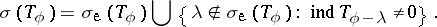 |
The following elementary results can be found in [a1].
If 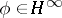 , then
, then 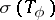 is the closure of
is the closure of 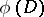 , where
, where 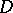 is the open unit disc (Wintner's theorem). If
is the open unit disc (Wintner's theorem). If 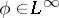 , then
, then
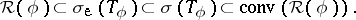 | (a1) |
Here, 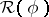 is the essential range of
is the essential range of 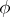 and
and 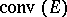 is the convex hull of a set
is the convex hull of a set 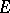 . Note that (a1) is a combination of an improvement of a Hartman–Wintner theorem and a Brown–Halmos theorem.
. Note that (a1) is a combination of an improvement of a Hartman–Wintner theorem and a Brown–Halmos theorem.
The following theorem, which is also due to P. Hartman and A. Wintner, describes the spectrum of self-adjoint Toeplitz operators (see [a1]): If 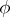 is a real function in
is a real function in 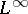 , then
, then
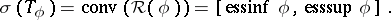 |
The problem of the invertibility of an arbitrary Toeplitz operator can be reduced to the case when the symbol is unimodular, i.e., has modulus 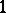 almost everywhere on
almost everywhere on 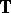 . Namely,
. Namely, 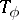 is invertible if and only if
is invertible if and only if 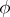 is invertible in
is invertible in 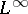 and the operator
and the operator 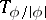 is invertible.
is invertible.
The following theorem is due to A. Devinatz, H. Widom and N.K. Nikol'skii, see [a1], [a5]: Let  be a unimodular function on
be a unimodular function on 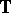 . Then
. Then
i) 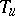 is left invertible if and only if
is left invertible if and only if 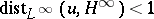 ;
;
ii) 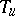 is right invertible if and only if
is right invertible if and only if 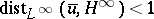 ;
;
iii) if 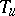 is invertible and there exists a function
is invertible and there exists a function 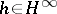 such that
such that 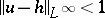 , then
, then 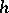 is invertible in
is invertible in 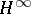 ;
;
iv) 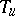 is invertible if and only if there exists an outer function (cf. also Hardy classes)
is invertible if and only if there exists an outer function (cf. also Hardy classes) 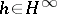 such that
such that 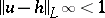 ;
;
v) if 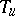 is left invertible, then
is left invertible, then 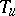 is invertible if and only if
is invertible if and only if 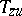 is not left invertible.
is not left invertible.
The following invertibility criterion was obtained independently by Widom and Devinatz, see [a1]: Let 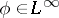 . Then
. Then 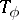 is invertible if and only if
is invertible if and only if 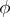 is invertible in
is invertible in 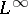 and the unimodular function
and the unimodular function 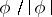 admits a representation
admits a representation
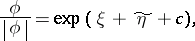 |
where 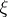 and
and 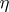 are real functions in
are real functions in 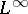 ,
, 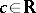 , and
, and 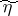 is the harmonic conjugate of
is the harmonic conjugate of 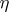 (cf. also Conjugate function).
(cf. also Conjugate function).
Note that this theorem is equivalent to the Helson–Szegö theorem on weighted boundedness of the harmonic conjugation operator.
The following general result was obtained by Widom for 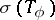 and improved by R.G. Douglas for
and improved by R.G. Douglas for 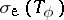 (see [a1]): Let
(see [a1]): Let 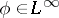 . Then
. Then 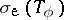 is a connected set. Consequently,
is a connected set. Consequently, 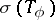 is connected.
is connected.
There is no geometric description of the spectrum of a general Toeplitz operator. However, for certain classes of functions 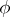 there exist nice geometric descriptions (see [a1]). For instance, let
there exist nice geometric descriptions (see [a1]). For instance, let 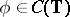 . Then
. Then 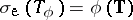 . If
. If 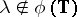 , then
, then
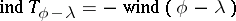 |
where 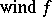 is the winding number of
is the winding number of 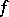 with respect to the origin.
with respect to the origin.
A similar result holds if 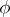 belongs to the algebra
belongs to the algebra 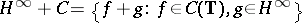 (Douglas' theorem, see [a1]): Let
(Douglas' theorem, see [a1]): Let 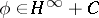 ; then
; then 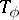 is a Fredholm operator if and only if
is a Fredholm operator if and only if 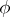 is invertible in
is invertible in 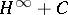 . If
. If 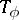 is Fredholm, then
is Fredholm, then
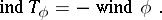 |
Note that if 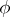 is invertible in
is invertible in 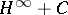 , then its harmonic extension to the unit disc
, then its harmonic extension to the unit disc 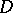 is separated away from
is separated away from  near the boundary
near the boundary 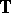 and
and  is, by definition, the winding number of the restriction of the harmonic extension of
is, by definition, the winding number of the restriction of the harmonic extension of 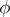 to a circle of radius sufficiently close to
to a circle of radius sufficiently close to 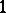 .
.
There is a similar geometric description of 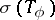 for piecewise-continuous functions
for piecewise-continuous functions 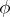 (the Devinatz–Widom theorem, see [a1]). In this case, instead of considering the curve
(the Devinatz–Widom theorem, see [a1]). In this case, instead of considering the curve  one has to consider the curve obtained from
one has to consider the curve obtained from 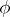 by adding intervals that join the points
by adding intervals that join the points 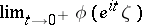 and
and 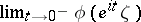 .
.
There are several local principles in the theory of Toeplitz operators. For 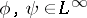 , the local distance at
, the local distance at 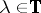 is defined by
is defined by
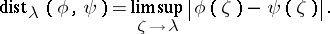 |
The Simonenko local principle (see [a5]) is as follows. Let 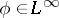 . Suppose that for each
. Suppose that for each 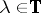 there exists a
there exists a 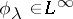 such that
such that 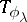 is Fredholm and
is Fredholm and 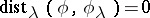 . Then
. Then 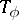 is Fredholm.
is Fredholm.
See [a1] for the Douglas localization principle.
If 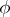 is a real
is a real 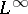 -function, the self-adjoint Toeplitz operator has absolutely continuous spectral measure ([a6]). In [a3] and [a7] an explicit description of the spectral type of
-function, the self-adjoint Toeplitz operator has absolutely continuous spectral measure ([a6]). In [a3] and [a7] an explicit description of the spectral type of  is given for
is given for 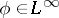 .
.
It is important in applications to study vectorial Toeplitz operators 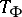 with matrix-valued symbols
with matrix-valued symbols 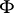 . There are vectorial Fredholm Toeplitz operators
. There are vectorial Fredholm Toeplitz operators 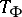 with zero index which are not invertible. If
with zero index which are not invertible. If 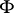 is a continuous matrix-valued function, then
is a continuous matrix-valued function, then 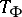 is Fredholm if and only if
is Fredholm if and only if 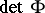 is invertible in
is invertible in 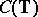 and
and
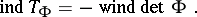 |
Similar results are valid for matrix-valued functions in  and for piecewise-continuous matrix-valued functions (see [a2]).
and for piecewise-continuous matrix-valued functions (see [a2]).
The following Simonenko theorem (see [a4]) gives a criterion for vectorial Toeplitz operators to be Fredholm. Let 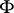 be an
be an 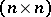 -matrix-valued
-matrix-valued 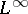 function on
function on 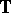 . Then
. Then 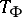 is Fredholm if and only if
is Fredholm if and only if  admits a factorization
admits a factorization
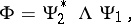 |
where 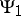 and
and 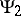 are matrix functions invertible in
are matrix functions invertible in 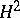 ,
,
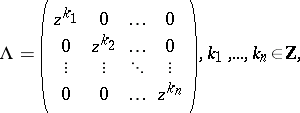 |
and the operator 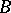 , defined on the set of polynomials in
, defined on the set of polynomials in 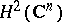 by
by
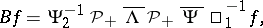 |
extends to a bounded operator on 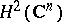 .
.
References
| [a1] | R.G. Douglas, "Banach algebra techniques in operator theory" , Acad. Press (1972) |
| [a2] | R.G. Douglas, "Banach algebra techniques in the theory of Toeplitz operators" , CBMS , 15 , Amer. Math. Soc. (1973) |
| [a3] | R.S. Ismagilov, "On the spectrum of Toeplitz matrices" Dokl. Akad. Nauk SSSR , 149 (1963) pp. 769–772 |
| [a4] | G.S. Litvinchuk, I.M. Spitkovski, "Factorization of measurable matrix functions" , Oper. Th. Adv. Appl. , 25 , Birkhäuser (1987) |
| [a5] | N.K. Nikol'skii, "Treatise on the shift operator" , Springer (1986) |
| [a6] | M. Rosenblum, "The absolute continuity of Toeplitz's matrices" Pacific J. Math. , 10 (1960) pp. 987–996 |
| [a7] | M. Rosenblum, "A concrete spectral theory for self-adjoint Toeplitz operators" Amer. J. Math. , 87 (1965) pp. 709–718 |
Toeplitz operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Toeplitz_operator&oldid=50002