There are many Toda systems spawned by Toda's nearest neighbour linking of anharmonic oscillators on the line [a1]. A convenient container is the  -Toda system, first introduced and studied comprehensively in [a2]; see also [a3].
-Toda system, first introduced and studied comprehensively in [a2]; see also [a3].
Let 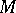 be a bi-infinite or semi-infinite matrix flowing as follows (
be a bi-infinite or semi-infinite matrix flowing as follows (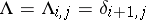 , the shift operator):
, the shift operator):
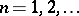 , with Borel decomposition
, with Borel decomposition
where 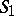 and
and 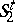 are lower triagonal and
are lower triagonal and 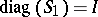 .
.
Define
then
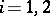 ;
; 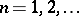 , with eigenvectors (
, with eigenvectors (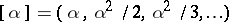 ,
, 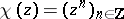 ):
):
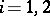 ;
; 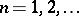 .
.
Let
the crucial identity
is equivalent to the bilinear identities for the tau-functions
which characterize the solution.
The 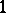 -Toda system (which can always be imbedded in the
-Toda system (which can always be imbedded in the  -Toda system) is just the
-Toda system) is just the  -flow for
-flow for 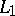 , i.e. it just involves ignoring
, i.e. it just involves ignoring 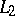 and in effect freezing
and in effect freezing 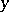 at one value. This is equivalent to the Grassmannian flag
at one value. This is equivalent to the Grassmannian flag 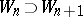 ,
, 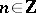 , where
, where
or, alternatively, it is characterized by the left-hand side of the bilinear identities 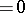 for
for 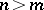 and
and 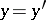 frozen (or suppressed). The semi-infinite (
frozen (or suppressed). The semi-infinite (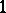 or
or  ) Toda system involves setting
) Toda system involves setting 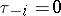 ,
, 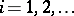 , and
, and  , in which case
, in which case 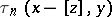 and
and 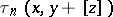 are polynomials in
are polynomials in  of degree at most
of degree at most  .
.
The famous triagonal Toda system — the original Toda system — is equivalent to the reduction 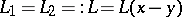 or, equivalently,
or, equivalently, 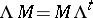 or, equivalently,
or, equivalently, 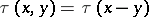 . In general, the
. In general, the 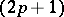 -gonal Toda system
-gonal Toda system 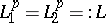 is equivalent to
is equivalent to 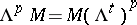 or, equivalently,
or, equivalently,
The 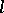 -periodic
-periodic  -Toda system is a
-Toda system is a  -Toda lattice such that
-Toda lattice such that 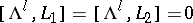 . One can of course consider more than one reduction at a time. For example, the
. One can of course consider more than one reduction at a time. For example, the 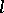 -periodic triagonal Toda lattice [a4] linearizes on the Jacobian of a hyper-elliptic curve
-periodic triagonal Toda lattice [a4] linearizes on the Jacobian of a hyper-elliptic curve 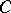 (the associated spectral curve) with the
(the associated spectral curve) with the 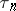 being essentially theta-functions
being essentially theta-functions 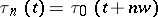 where
where 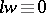 in
in 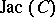 ,
, 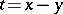 , the flat coordinates on
, the flat coordinates on 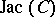 .
.
One can also consider in this context Toda flows going with different Lie algebras:
where 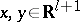 ,
, 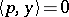 , with
, with 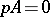 ,
, 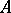 being the Cartan matrix of Kac–Moody Lie algebras by extended Dynkin diagrams (cf. also Kac–Moody algebra). The non-periodic case involves
being the Cartan matrix of Kac–Moody Lie algebras by extended Dynkin diagrams (cf. also Kac–Moody algebra). The non-periodic case involves 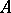 being the Cartan matrix of a simple Lie algebra, in which case
being the Cartan matrix of a simple Lie algebra, in which case 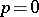 . The former case linearizes on Abelian varieties [a4] and the latter on "non-compact" Abelian varieties [a5].
. The former case linearizes on Abelian varieties [a4] and the latter on "non-compact" Abelian varieties [a5].
References
| [a1] | M. Toda, "Vibration of a chain with a non-linear interaction" J. Phys. Soc. Japan , 22 (1967) pp. 431–436 |
| [a2] | K. Ueno, K. Takasaki, "Toda lattice hierarchy" Adv. Studies Pure Math. , 4 (1984) pp. 1–95 |
| [a3] | M. Adler, P. van Moerbeke, "Group factorization, moment matrices and Toda latices" Internat. Math. Research Notices , 12 (1997) |
| [a4] | M. Adler, P. van Moerbeke, "Completely integrable systems, Euclidean Lie algebras and curves; Linearization of Hamiltonians systems, Jacoby varieties and representation theory" Adv. Math. , 38 (1980) pp. 267–379 |
| [a5] | B. Konstant, "The solution to a generalized Toda lattice and representation theory" Adv. Math. , 34 (1979) pp. 195–338 |
How to Cite This Entry:
Toda lattices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Toda_lattices&oldid=49931
This article was adapted from an original article by M. Adler (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article -Toda system, first introduced and studied comprehensively in [a2]; see also [a3].
-Toda system, first introduced and studied comprehensively in [a2]; see also [a3].
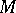 be a bi-infinite or semi-infinite matrix flowing as follows (
be a bi-infinite or semi-infinite matrix flowing as follows (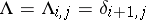 , the shift operator):
, the shift operator):
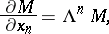
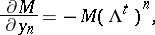
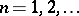 , with Borel decomposition
, with Borel decomposition
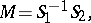
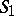 and
and 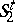 are lower triagonal and
are lower triagonal and 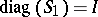 .
.
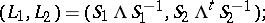
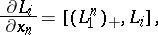
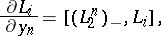
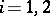 ;
; 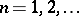 , with eigenvectors (
, with eigenvectors (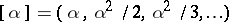 ,
, 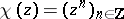 ):
):
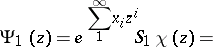
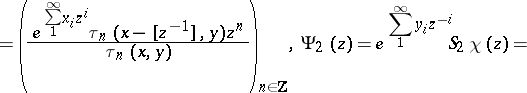
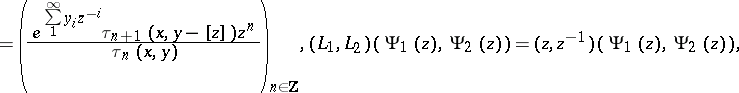
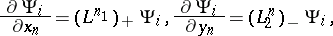
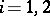 ;
; 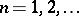 .
.
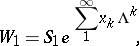
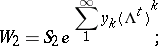
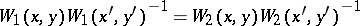
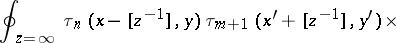
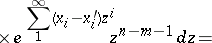
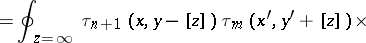
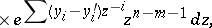
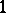 -Toda system (which can always be imbedded in the
-Toda system (which can always be imbedded in the  -Toda system) is just the
-Toda system) is just the  -flow for
-flow for 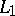 , i.e. it just involves ignoring
, i.e. it just involves ignoring 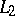 and in effect freezing
and in effect freezing 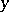 at one value. This is equivalent to the Grassmannian flag
at one value. This is equivalent to the Grassmannian flag 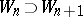 ,
, 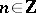 , where
, where
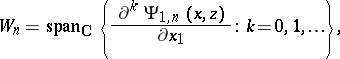
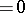 for
for 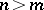 and
and 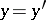 frozen (or suppressed). The semi-infinite (
frozen (or suppressed). The semi-infinite (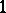 or
or  ) Toda system involves setting
) Toda system involves setting 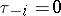 ,
, 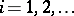 , and
, and  , in which case
, in which case 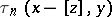 and
and 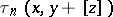 are polynomials in
are polynomials in  of degree at most
of degree at most  .
.
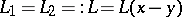 or, equivalently,
or, equivalently, 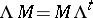 or, equivalently,
or, equivalently, 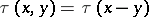 . In general, the
. In general, the 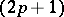 -gonal Toda system
-gonal Toda system 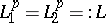 is equivalent to
is equivalent to 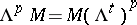 or, equivalently,
or, equivalently,
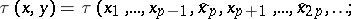
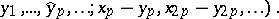
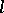 -periodic
-periodic  -Toda system is a
-Toda system is a  -Toda lattice such that
-Toda lattice such that 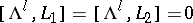 . One can of course consider more than one reduction at a time. For example, the
. One can of course consider more than one reduction at a time. For example, the 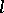 -periodic triagonal Toda lattice [a4] linearizes on the Jacobian of a hyper-elliptic curve
-periodic triagonal Toda lattice [a4] linearizes on the Jacobian of a hyper-elliptic curve 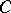 (the associated spectral curve) with the
(the associated spectral curve) with the 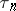 being essentially theta-functions
being essentially theta-functions 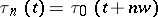 where
where 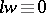 in
in 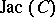 ,
, 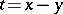 , the flat coordinates on
, the flat coordinates on 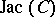 .
.
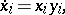
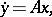
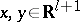 ,
, 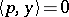 , with
, with 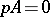 ,
, 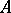 being the Cartan matrix of Kac–Moody Lie algebras by extended Dynkin diagrams (cf. also Kac–Moody algebra). The non-periodic case involves
being the Cartan matrix of Kac–Moody Lie algebras by extended Dynkin diagrams (cf. also Kac–Moody algebra). The non-periodic case involves 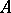 being the Cartan matrix of a simple Lie algebra, in which case
being the Cartan matrix of a simple Lie algebra, in which case 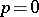 . The former case linearizes on Abelian varieties [a4] and the latter on "non-compact" Abelian varieties [a5].
. The former case linearizes on Abelian varieties [a4] and the latter on "non-compact" Abelian varieties [a5].