Natural operator in differential geometry

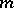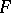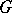In the simplest case, one considers two natural bundles over -dimensional manifolds and , cf. Natural transformation in differential geometry. A natural operator is a system of operators 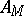transforming every section of 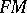into a section 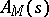of 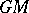for every 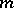-dimensional manifold 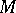with the following properties:

1) 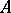commutes with the action of diffeomorphisms, i.e.

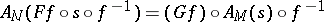for every diffeomorphism ;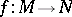

2) 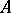has the localization property, i.e. 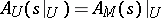for every open subset ;

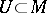3) 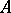is regular, i.e. every smoothly parametrized family of sections is transformed into a smoothly parametrized family.

This idea has been generalized to other categories over manifolds and to operators defined on certain distinguished classes of sections in [a2].

The 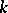th order natural operators 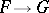are in bijection with the natural transformations of the 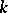th jet prolongation 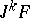into 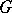. In this case the methods from [a2] can be applied for finding natural operators. So it is important to have some criteria guaranteeing that all natural operators of a prescribed type have finite order. Fundamental results in this direction were deduced by J. Slovák, who developed a far-reaching generalization of the Peetre theorem to non-linear problems, [a2]. However, in certain situations there exist natural operators of infinite order.

The first result about natural operators was deduced by R. Palais, [a3], who proved that all linear natural operators transforming exterior 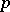-forms into exterior 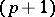-forms are constant multiples of the exterior differential (cf. also Exterior form). In [a2] new methods are used to prove that for 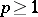linearity even follows from naturality.

Many concrete problems on finding all natural operators are solved in [a2].

The following result on the natural operators on morphisms of fibred manifolds is closely related to the geometry of the calculus of variations. On a fibred manifold with 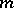-dimensional base, 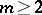, there is no natural operator transforming th order Lagrangeans into Poincaré–Cartan morphisms for 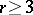, see [a1]. In this case, one has to use an additional structure to distinguish a single Poincaré-Cartan form determined by a Lagrangean.

References

[a1]	I. Kolář, "Natural operators related with the variational calculus" , Proc. Conf. Diff. Geom. Appl., Silesian Univ. Opava (1993) pp. 461–472
[a2]	I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993)
[a3]	R. Palais, "Natural operations on differential forms" Trans. Amer. Math. Soc. , 92 (1959) pp. 125–141