Quantum homogeneous space
A unital algebra  that is a co-module for a quantum group
that is a co-module for a quantum group  (cf. Quantum groups) and for which the structure mapping
(cf. Quantum groups) and for which the structure mapping  is an algebra homomorphism, i.e.,
is an algebra homomorphism, i.e.,  is a co-module algebra [a1]. Here,
is a co-module algebra [a1]. Here,  is a deformation of the Poisson algebra
is a deformation of the Poisson algebra  , of a Poisson–Lie group
, of a Poisson–Lie group  , endowed with the structure of a Hopf algebra with a co-multiplication
, endowed with the structure of a Hopf algebra with a co-multiplication  and a co-unit
and a co-unit  . Often, both
. Often, both 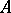 and
and 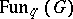 can also be equipped with a
can also be equipped with a  -involution. The left co-action
-involution. The left co-action 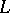 satisfies
satisfies
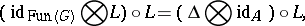 |
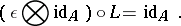 |
These relations should be modified correspondingly for a right co-action. In the dual picture, if 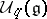 is the deformed universal enveloping algebra of the Lie algebra
is the deformed universal enveloping algebra of the Lie algebra 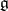 and
and 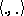 is a non-degenerate dual pairing between the Hopf algebras
is a non-degenerate dual pairing between the Hopf algebras 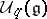 and
and  , then the prescription
, then the prescription 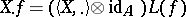 , with
, with  and
and  , defines a right action of
, defines a right action of 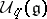 on
on 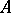 (
(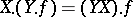 ) and one has
) and one has
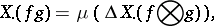 |
where 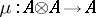 is the multiplication in
is the multiplication in 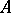 and
and 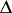 is the co-multiplication in
is the co-multiplication in 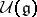 . Typically,
. Typically, 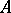 is a deformation of the Poisson algebra
is a deformation of the Poisson algebra 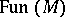 (frequently called the quantization of
(frequently called the quantization of  ), where
), where 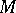 is a Poisson manifold and, at the same time, a left homogeneous space of
is a Poisson manifold and, at the same time, a left homogeneous space of 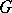 with the left action
with the left action 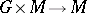 a Poisson mapping.
a Poisson mapping.
It is not quite clear how to translate into purely algebraic terms the property that 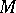 is a homogeneous space of
is a homogeneous space of 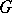 . One possibility is to require that only multiples of the unit
. One possibility is to require that only multiples of the unit 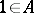 satisfy
satisfy 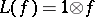 . A stronger condition requires the existence of a linear functional
. A stronger condition requires the existence of a linear functional 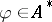 such that
such that  while the linear mapping
while the linear mapping 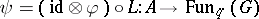 be injective. Then
be injective. Then 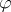 can be considered as a base point.
can be considered as a base point.
The still stronger requirement that, in addition, 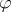 be a homomorphism (a so-called classical point) holds when
be a homomorphism (a so-called classical point) holds when 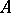 is a quantization of a Poisson homogeneous space
is a quantization of a Poisson homogeneous space 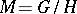 with
with 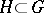 a Poisson–Lie subgroup. The quantum homogeneous space
a Poisson–Lie subgroup. The quantum homogeneous space  is defined as the subalgebra in
is defined as the subalgebra in 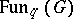 formed by
formed by 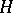 -invariant elements
-invariant elements  ,
,  where
where 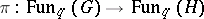 is a Hopf-algebra homomorphism.
is a Hopf-algebra homomorphism.
A richer class of examples is provided by quantization of orbits of the dressing transformation of 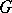 , acting on its dual Poisson–Lie group (also called the generalized Pontryagin dual)
, acting on its dual Poisson–Lie group (also called the generalized Pontryagin dual) 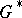 . The best studied cases concern the compact and solvable factors
. The best studied cases concern the compact and solvable factors 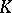 and
and 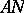 (
(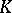 and
and 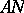 are mutually dual) in the Iwasawa decomposition
are mutually dual) in the Iwasawa decomposition  , where
, where 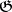 is a simple complex Lie group. One obtains this way, among others, the quantum sphere and, more generally, quantum Grassmannian and quantum flag manifolds.
is a simple complex Lie group. One obtains this way, among others, the quantum sphere and, more generally, quantum Grassmannian and quantum flag manifolds.
There is a vast amount of literature on this subject. The survey book [a2] contains a rich list of references.
References
| [a1] | E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977) |
| [a2] | V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994) |
Quantum homogeneous space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_homogeneous_space&oldid=49876