Wilcoxon test

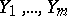A non-parametric test of the homogeneity of two samples and . The elements of the samples are assumed to be mutually independent, with continuous distribution functions 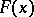and 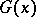, respectively. The hypothesis to be tested is 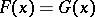. Wilcoxon's test is based on the rank statistic

(*)

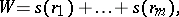where 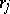are the ranks of the random variables in the common series of order statistics of 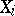and 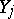, while the function 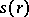, , 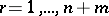is defined by a given permutation

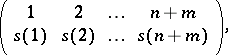where is one of the possible rearrangements of the numbers 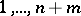. The permutation is chosen so that the power of Wilcoxon's test for the given alternative is highest. The statistical distribution of depends only on the size of the samples and not on the chosen permutation (if the homogeneity hypothesis is true). If 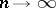and 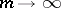, the random variable has an asymptotically-normal distribution. This variant of the test was first proposed by F. Wilcoxon in 1945 for samples of equal sizes and was based on the special case 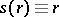(cf. Rank sum test; Mann–Whitney test). See also van der Waerden test; Rank test.

References

[1]	F. Wilcoxon, "Individual comparison by ranking methods" Biometrics , 1 : 6 (1945) pp. 80–83
[2]	L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)
[3]	B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)

References

[a1]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)