Weierstrass conditions (for a variational extremum)

Necessary and (partially) sufficient conditions for a strong extremum in the classical calculus of variations (cf. Variational calculus). Proposed in 1879 by K. Weierstrass.

Weierstrass' necessary condition: For the functional

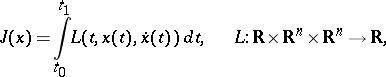to attain a strong local minimum on the extremal 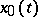, it is necessary that the inequality

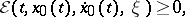where 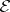is the Weierstrass 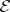-function, be satisfied for all , , 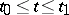and all 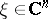. This condition may be expressed in terms of the function

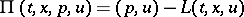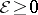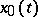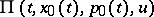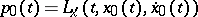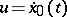(cf. Pontryagin maximum principle). The Weierstrass condition ( on the extremal ) is equivalent to saying that the function , where , attains a maximum in for . Thus, Weierstrass' necessary condition is a special case of the Pontryagin maximum principle.

Weierstrass' sufficient condition: For the functional

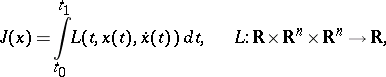to attain a strong local minimum on the vector function 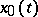, it is sufficient that there exists a vector-valued field slope function 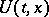(geodesic slope) (cf. Hilbert invariant integral) in a neighbourhood 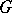of the curve 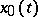, for which

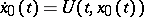and

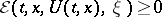for all 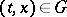and any vector .

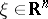References

[1]	M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian)
[2]	G.A. Bliss, "Lectures on the calculus of variations" , Chicago Univ. Press (1947)
[3]	L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Wiley (1962) (Translated from Russian)

Comments

See also Weierstrass–Erdmann corner conditions, for necessary conditions at a corner of an extremal.

References

[a1]	I.M. Gel'fand, S.V. Fomin, "Calculus of variations" , Prentice-Hall (1963) (Translated from Russian)
[a2]	L. Cesari, "Optimization - Theory and applications" , Springer (1983)