Weierstrass-Erdmann corner conditions
Necessary conditions for an extremum, additional to the Euler equation, specified at points at which the extremal has a corner. Let
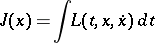 |
be a functional of the classical calculus of variations (cf. Variational calculus), and let the extremal 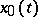 be continuously differentiable in a neighbourhood of the point
be continuously differentiable in a neighbourhood of the point  except at the point
except at the point  itself, at which it has a corner. In this situation, for
itself, at which it has a corner. In this situation, for  to be at least a weak local extremum for the functional
to be at least a weak local extremum for the functional 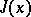 , it is necessary that the equations
, it is necessary that the equations
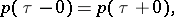 |
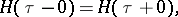 |
where
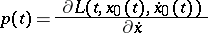 |
and
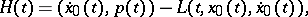 |
be satisfied at the corner point  . These equations are known as the corner conditions of K. Weierstrass (1865) and G. Erdmann (1877) [1].
. These equations are known as the corner conditions of K. Weierstrass (1865) and G. Erdmann (1877) [1].
The meaning of the Weierstrass–Erdmann corner conditions is that the canonical variables and the Hamiltonian are continuous at a corner point of the extremal; their meaning in classical mechanics is the continuity of momentum and of energy at a corner point.
In regular problems, when 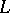 is a strictly convex function of
is a strictly convex function of 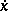 , the extremals cannot have corner points. Corner points appear if
, the extremals cannot have corner points. Corner points appear if 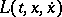 and consequently the Weierstrass
and consequently the Weierstrass 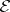 -function, contains segments of
-function, contains segments of 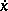 . For the Lagrange problem with conditions
. For the Lagrange problem with conditions 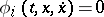 and Lagrange multipliers
and Lagrange multipliers 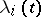 , the
, the  in the Weierstrass–Erdmann corner conditions is replaced by
in the Weierstrass–Erdmann corner conditions is replaced by 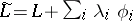 .
.
References
| [1] | G. Erdmann, "Ueber die unstetige Lösungen in der Variationsrechnung" J. Reine Angew. Math. , 82 (1877) pp. 21–30 |
| [2] | O. Bolza, "Lectures on the calculus of variations" , Chelsea, reprint (1960) (Translated from German) |
| [3] | N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian) |
Comments
See also Weierstrass conditions (for a variational extremum).
References
| [a1] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
| [a2] | G.M. Ewing, "Calculus of variations with applications" , Dover, reprint (1985) |
| [a3] | Yu.P. Petrov, "Variational methods in optimum control theory" , Acad. Press (1968) pp. Chapt. IV (Translated from Russian) |
Weierstrass-Erdmann corner conditions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass-Erdmann_corner_conditions&oldid=49188