Watson transform
An integral transform 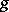 of a function
of a function 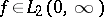 , defined as follows:
, defined as follows:
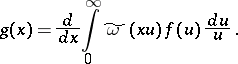 | (1) |
Here  is a real variable, the kernel
is a real variable, the kernel 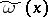 has the form
has the form
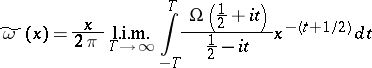 | (2) |
(l.i.m. denotes the limit in the mean in 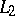 ) and the function
) and the function 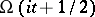 satisfies the condition
satisfies the condition
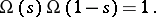 |
The following conditions are sufficient for the existence of the kernel 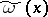 and the inclusion
and the inclusion 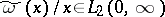 :
:
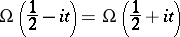 |
and
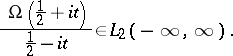 |
For a function 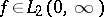 , formula (1) defines the function
, formula (1) defines the function 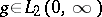 almost-everywhere. The inversion formula for the Watson transform (1) has the form
almost-everywhere. The inversion formula for the Watson transform (1) has the form
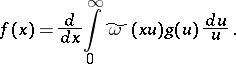 |
Named after G.N. Watson [1], who was the first to study this transform.
References
| [1] | G.N. Watson, "General transforms" Proc. London Math. Soc. (2) , 35 (1933) pp. 156–199 |
Comments
Quite generally, let 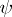 be a Lebesgue-measure function in
be a Lebesgue-measure function in 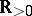 and let
and let
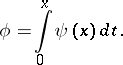 |
The kernel 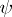 (or
(or  ) is called a generalized kernel, or kernel of a generalized transform, if
) is called a generalized kernel, or kernel of a generalized transform, if
a) 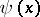 is real valued on
is real valued on 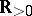 ;
;
b) 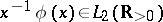 ;
;
c) 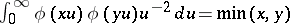 .
.
The operator 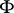 defined on
defined on 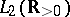 by
by
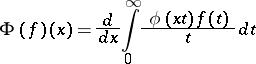 |
is called a generalized transform or Watson transform.
References
| [a1] | G.O. Okikiolu, "Aspects of the theory of bounded operators in 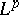 -spaces" , Acad. Press (1971) pp. §6.7 -spaces" , Acad. Press (1971) pp. §6.7 |
Watson transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Watson_transform&oldid=49174