Upper bound of a family of topologies
least upper bound, on a set 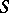
The topology 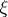 which is the finest of all topologies on
which is the finest of all topologies on 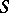 containing all topologies of the given family
containing all topologies of the given family 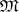 (cf. Comparison of topologies). A subbase of the topology
(cf. Comparison of topologies). A subbase of the topology 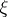 is formed by the family of all subsets of
is formed by the family of all subsets of 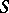 which are open in at least one topology of the family
which are open in at least one topology of the family 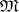 .
.
The family of all possible topologies on the set 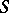 with the operation defined above, which consists in taking the upper bound of any subfamily, and a minimal element — the trivial topology — is a complete lattice. The upper bound of a family of topologies is also known as the inductive limit of a family of topologies.
with the operation defined above, which consists in taking the upper bound of any subfamily, and a minimal element — the trivial topology — is a complete lattice. The upper bound of a family of topologies is also known as the inductive limit of a family of topologies.
The following interpretation of the upper bound of a family of topologies is useful. Let
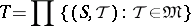 |
be the Tikhonov product of all topological spaces which result from imparting the various topologies in the family 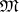 to the set
to the set 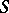 . Let
. Let  be the diagonal of this product, i.e. the set of all constant mappings from
be the diagonal of this product, i.e. the set of all constant mappings from 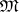 into
into 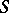 (or, which is the same thing, the set of all threads (cf. Thread)
(or, which is the same thing, the set of all threads (cf. Thread) 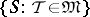 for which
for which  for all
for all 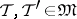 ). The set
). The set  is in a natural one-to-one correspondence with the set
is in a natural one-to-one correspondence with the set  (this can be seen by projecting the set
(this can be seen by projecting the set 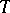 onto any of its factors). If
onto any of its factors). If 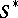 is equipped with the topology induced from the space
is equipped with the topology induced from the space 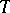 , and if this topology is transferred to
, and if this topology is transferred to 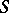 using the correspondence mentioned above, one obtains the upper bound of the family
using the correspondence mentioned above, one obtains the upper bound of the family 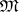 . This interpretation of the upper bound of a family of topologies makes it possible to understand that the upper bound of any family of Hausdorff topologies is a Hausdorff topology, and the upper bound of any family of (completely) regular topologies is a (completely) regular topology. Similar statements do not apply to families of normal and paracompact topologies. However, the upper bound of a countable family of metrizable topologies (with a countable base) is a metrizable topology (with a countable base). The diagonal
. This interpretation of the upper bound of a family of topologies makes it possible to understand that the upper bound of any family of Hausdorff topologies is a Hausdorff topology, and the upper bound of any family of (completely) regular topologies is a (completely) regular topology. Similar statements do not apply to families of normal and paracompact topologies. However, the upper bound of a countable family of metrizable topologies (with a countable base) is a metrizable topology (with a countable base). The diagonal  is, as a rule, not closed in
is, as a rule, not closed in 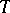 , and for this reason the upper bound of two compact topologies is not necessarily compact.
, and for this reason the upper bound of two compact topologies is not necessarily compact.
References
| [1] | J.L. Kelley, "General topology" , Springer (1975) |
| [2] | N. Bourbaki, "Elements of mathematics. General topology" , Springer (1989) (Translated from French) |
Upper bound of a family of topologies. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Upper_bound_of_a_family_of_topologies&oldid=49098