Unitary operator
From Encyclopedia of Mathematics
A linear operator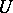 
mapping a normed linear space 
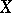onto a normed linear space 
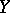such that 
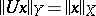. The most important unitary operators are those mapping a Hilbert space onto itself. Such an operator is unitary if and only if 
for all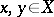 
. Other characterizations of a unitary operator 
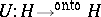are: 1) 
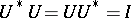, i.e. 
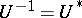; and 2) the spectrum of 
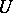lies on the unit circle and there is the spectral decomposition 
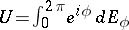. The set of unitary operators acting on 
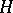forms a group.
Examples of unitary operators and their inverses on the space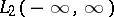 
are the Fourier transform and its inverse.
References
| [1] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
| [2] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1 , Pitman (1980) (Translated from Russian) |
| [3] | A.I. Plessner, "Spectral theory of linear operators" , F. Ungar (1965) (Translated from Russian) |
How to Cite This Entry:
Unitary operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_operator&oldid=49084
Unitary operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_operator&oldid=49084
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article