Unitary matrix

A square matrix over the field of complex numbers, whose rows form an orthonormal system, i.e.

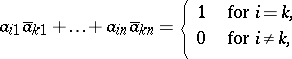. In a unitary space, transformation from one orthonormal basis to another is accomplished by a unitary matrix. The matrix of a unitary transformation relative to an orthonormal basis is also (called) a unitary matrix. A square matrix with complex entries is unitary if and only if it satisfies any of the following conditions:

1) ;

2) ;

3) ;

4) the columns of form an orthonormal system (here is the conjugate transposed of ).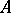

The determinant of a unitary matrix is a complex number of modulus one.

References

[a1]	W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. 63
[a2]	W.H. Greub, "Linear algebra" , Springer (1975) pp. 329