Uniqueness properties of analytic functions
Properties of analytic functions that say that they are completely determined by their values on certain subsets of their domain of definition, or of its boundary; in this connection one may distinguish interior uniqueness properties and boundary uniqueness properties.
Interior uniqueness properties.
Let 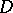 be a domain in the complex plane
be a domain in the complex plane 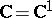 . The classical interior uniqueness theorem for holomorphic (that is, single-valued analytic) functions on
. The classical interior uniqueness theorem for holomorphic (that is, single-valued analytic) functions on 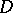 states that if two holomorphic functions
states that if two holomorphic functions 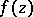 and
and 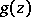 in
in 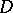 coincide on some set
coincide on some set 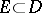 containing at least one limit point in
containing at least one limit point in 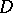 , then
, then 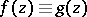 everywhere in
everywhere in 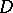 . In other words, if a holomorphic function
. In other words, if a holomorphic function 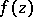 in
in 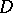 vanishes on a set
vanishes on a set 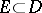 having at least one limit point in
having at least one limit point in 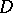 , then
, then 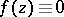 . The proof of this interior uniqueness property of analytic functions shows that it is essentially a uniqueness property of power series in one complex variable
. The proof of this interior uniqueness property of analytic functions shows that it is essentially a uniqueness property of power series in one complex variable  . The uniqueness property remains valid for meromorphic functions
. The uniqueness property remains valid for meromorphic functions 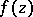 and
and 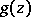 in
in 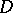 if one regards the poles of
if one regards the poles of 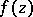 and
and 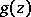 as points at which the functions take the value
as points at which the functions take the value 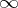 .
.
In particular, if two analytic functions 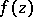 and
and 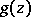 coincide in an arbitrarily small neighbourhood of some point or on an arbitrarily small arc of some continuous curve, then
coincide in an arbitrarily small neighbourhood of some point or on an arbitrarily small arc of some continuous curve, then 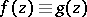 . Another corollary: The set of
. Another corollary: The set of 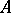 -points of an analytic function
-points of an analytic function 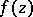 , that is, the set of points
, that is, the set of points  at which
at which 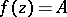 , cannot have limit points inside the domain of definition
, cannot have limit points inside the domain of definition 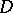 , provided that
, provided that 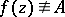 .
.
Two complete analytic functions in the sense of Weierstrass (cf. Complete analytic function) 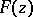 ,
,  are, in general, multiple valued, and have the following interior uniqueness property: Let
are, in general, multiple valued, and have the following interior uniqueness property: Let 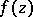 ,
, 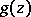 be single-valued elements, or branches, of
be single-valued elements, or branches, of 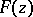 and
and 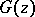 , defined on domains
, defined on domains 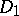 and
and 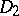 , respectively, with
, respectively, with  . If
. If 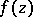 and
and 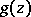 coincide on some set
coincide on some set 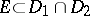 having at least one limit point
having at least one limit point 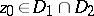 , then
, then 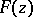 and
and 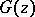 have the same domain of existence and coincide everywhere as complete analytic functions.
have the same domain of existence and coincide everywhere as complete analytic functions.
These formulations of uniqueness properties do not carry over to the case of functions 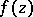 of several complex variables
of several complex variables 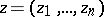 ,
, 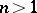 . For example, the analytic function
. For example, the analytic function 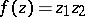 is not identically zero, but vanishes on the analytic planes
is not identically zero, but vanishes on the analytic planes  and
and  of complex dimension
of complex dimension 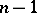 . The following uniqueness properties hold for such functions:
. The following uniqueness properties hold for such functions:
1) If 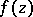 is an analytic function on a domain
is an analytic function on a domain 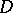 of the complex space
of the complex space 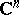 and vanishes at all points of some non-empty open subset
and vanishes at all points of some non-empty open subset 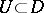 , then
, then 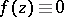 on
on 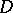 .
.
2) If  is an analytic function on a domain
is an analytic function on a domain 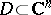 that vanishes at some point
that vanishes at some point 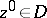 together with all its partial derivatives
together with all its partial derivatives  ,
, 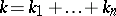 ;
; 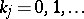 ;
;  , then
, then 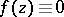 on
on 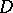 .
.
3) If  is an analytic function on a domain
is an analytic function on a domain 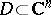 that vanishes in a real neighbourhood
that vanishes in a real neighbourhood 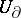 of a point
of a point  , that is, on a set
, that is, on a set 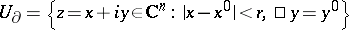 , then
, then 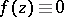 on
on 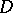 .
.
The difference between interior uniqueness properties in the cases  and
and 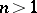 is caused by the different behaviour of power series in one and in several variables.
is caused by the different behaviour of power series in one and in several variables.
Boundary uniqueness properties.
The uniqueness theorem stated above for an analytic function  of a single complex variable admits several generalizations to the case when the zeros of
of a single complex variable admits several generalizations to the case when the zeros of  do not lie in the interior of the domain
do not lie in the interior of the domain 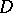 of analyticity, but on its boundary
of analyticity, but on its boundary 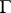 . The most general and deepest boundary uniqueness theorems were obtained by N.N. Luzin and I.I. Privalov in 1925 (cf. also Luzin–Privalov theorems). Let
. The most general and deepest boundary uniqueness theorems were obtained by N.N. Luzin and I.I. Privalov in 1925 (cf. also Luzin–Privalov theorems). Let 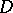 be a domain in the
be a domain in the  -plane bounded by a rectifiable curve
-plane bounded by a rectifiable curve  , and let
, and let  be a meromorphic function in
be a meromorphic function in 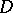 . Let
. Let  be a point of
be a point of  at which the tangent to
at which the tangent to 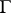 exists; almost-all points of a rectifiable curve have this property. One says that
exists; almost-all points of a rectifiable curve have this property. One says that  has an angular boundary value
has an angular boundary value  at
at  if
if  tends to
tends to 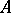 as
as  tends to
tends to  remaining within the intersection of the domain
remaining within the intersection of the domain  and the interior of any angle less than
and the interior of any angle less than 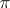 with vertex
with vertex  having the normal to
having the normal to 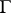 at
at 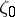 as its bisector.
as its bisector.
The Luzin–Privalov boundary uniqueness theorem for angular boundary values then holds: If 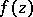 is meromorphic in a domain
is meromorphic in a domain 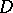 bounded by a rectifiable curve
bounded by a rectifiable curve 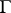 and takes angular boundary values zero on a set
and takes angular boundary values zero on a set 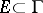 of positive Lebesgue measure, then
of positive Lebesgue measure, then 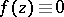 . In general, a meromorphic function need not have boundary values on
. In general, a meromorphic function need not have boundary values on 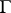 . But for a fairly large class of meromorphic functions, for example, for functions of bounded characteristic, the existence of angular boundary values almost everywhere on
. But for a fairly large class of meromorphic functions, for example, for functions of bounded characteristic, the existence of angular boundary values almost everywhere on 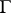 has been established.
has been established.
Along with these, there are examples of bounded analytic functions in the unit disc 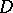 that converge to zero in all senses on a given set of points
that converge to zero in all senses on a given set of points  of measure zero on the unit circle
of measure zero on the unit circle 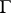 . Moreover, Luzin and Privalov have also constructed examples of analytic functions in the unit disc
. Moreover, Luzin and Privalov have also constructed examples of analytic functions in the unit disc 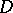 having zero radial boundary values, that is, tending to zero along radii, everywhere on a set
having zero radial boundary values, that is, tending to zero along radii, everywhere on a set 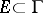 of full measure
of full measure 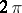 . It turns out that in uniqueness problems the concept of the Baire category of a set is also very important. In fact, there is a Luzin–Privalov boundary uniqueness theorem for radial boundary values: If the function
. It turns out that in uniqueness problems the concept of the Baire category of a set is also very important. In fact, there is a Luzin–Privalov boundary uniqueness theorem for radial boundary values: If the function 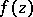 is meromorphic in the unit disc
is meromorphic in the unit disc 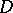 , has radial boundary values zero on a set
, has radial boundary values zero on a set 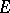 situated on an arc
situated on an arc  of the unit circle
of the unit circle 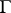 , and if
, and if 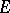 is metrically dense and of the second Baire category in
is metrically dense and of the second Baire category in 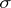 , then
, then 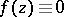 . (A set
. (A set 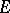 is called metrically dense in
is called metrically dense in 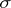 if the intersection of
if the intersection of 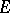 with each subarc of
with each subarc of 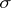 has positive measure.)
has positive measure.)
See also Boundary properties of analytic functions; Limit set.
The investigation of boundary uniqueness properties of analytic functions of several complex variables has not yet achieved the same degree of completeness as for functions of a single variable (see [5], [6]).
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Chapt. 3 (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) pp. Chapt. 2 (In Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) |
| [5] | W. Rudin, "Function theory in the polydisc" , Benjamin (1969) |
| [6] | G.M. [G.M. Khenkin] Henkin, E.M. [E.M. Chirka] Čirka, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 (1976) pp. 612–687 Itogi Nauk. Sovrem. Probl. Mat. , 4 (1975) pp. 13–142 |
| [7] | W. Rudin, "Function theory in the unit ball in 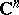 " , Springer (1980) " , Springer (1980) |
| [8] | P. Koosis, "Introduction to 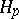 -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) |
Comments
Analogues of the Luzin–Privalov examples of holomorphic functions, not identically equal to zero and with radial boundary values zero almost everywhere, have been found for the unit ball in 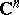 too, see [a1].
too, see [a1].
References
| [a1] | M. Hakim, N. Sibony, "Boundary properties of holomorphic functions in the ball in  " Math. Ann. , 276 (1987) pp. 549–555 " Math. Ann. , 276 (1987) pp. 549–555 |
Uniqueness properties of analytic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniqueness_properties_of_analytic_functions&oldid=49082