Gegenbauer polynomials
Orthogonal polynomials  on the interval
on the interval  with the weight function
with the weight function  ; a particular case of the Jacobi polynomials for
; a particular case of the Jacobi polynomials for  (
( ); the Legendre polynomials
); the Legendre polynomials  are a particular case of the ultraspherical polynomials:
are a particular case of the ultraspherical polynomials:  .
.
For ultraspherical polynomials one has the standardization
and the representation
The ultraspherical polynomials are the coefficients of the power series expansion of the generating function
The ultraspherical polynomial 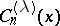 satisfies the differential equation
satisfies the differential equation
More commonly used are the formulas
For references see Orthogonal polynomials.
See Spherical harmonics for a group-theoretic interpretation. Ultraspherical polynomials are also connected with Jacobi polynomials by the quadratic transformations
See [a1] for  -ultraspherical polynomials.
-ultraspherical polynomials.
References
| [a1] | R.A. Askey, M.E.H. Ismail, "A generalization of ultraspherical polynomials" P. Erdös (ed.) , Studies in Pure Mathematics to the Memory of Paul Turán , Birkhäuser (1983) pp. 55–78 |
How to Cite This Entry:
Ultraspherical polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ultraspherical_polynomials&oldid=49062
This article was adapted from an original article by P.K. Suetin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article on the interval
on the interval  with the weight function
with the weight function  ; a particular case of the Jacobi polynomials for
; a particular case of the Jacobi polynomials for  (
( ); the Legendre polynomials
); the Legendre polynomials  are a particular case of the ultraspherical polynomials:
are a particular case of the ultraspherical polynomials:  .
.
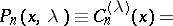
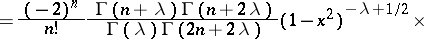
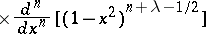
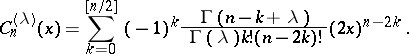
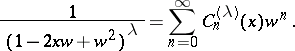
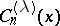 satisfies the differential equation
satisfies the differential equation
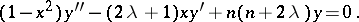

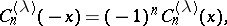
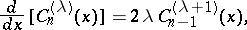
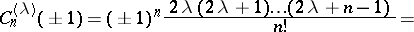
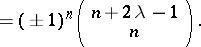
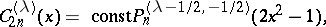
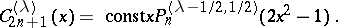
 -ultraspherical polynomials.
-ultraspherical polynomials.