Tricomi problem

The problem related to the existence of solutions for differential equations of mixed elliptic-hyperbolic type with two independent variables in an open domain of special shape. The domain can be decomposed into the union of two subdomains 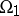and 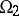by a smooth simple curve 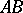whose end points 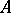and 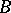are different points of 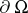. The equation is elliptic in 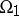, hyperbolic in 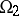, and degenerates to parabolic on the curve 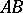. The boundary 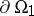is the union of the curve 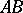and a smooth simple curve 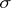, while 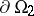is the union of characteristics 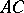and 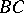and the curve 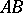. The desired solution must take prescribed data on 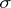and on only one of the characteristics 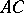and 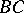(see Mixed-type differential equation).

The Tricomi problem for the Tricomi equation

(1)

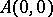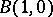was first posed and studied by F. Tricomi [1], [2]. The domain is bounded by a smooth curve with end points , and characteristics 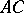and :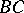

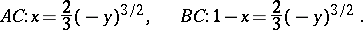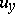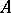Under specified restrictions on the smoothness of the given functions and the behaviour of the derivative of the solution at the points and 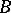, the Tricomi problem

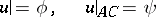(2)

for equation (1) reduces to finding the solution 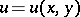of equation (1) that is regular in the domain 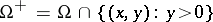and that satisfies the boundary conditions

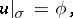(3)

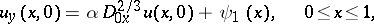where 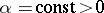, 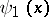is uniquely determined by 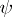, 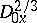is the fractional differentiation operator of order 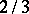(in the sense of Riemann–Liouville):

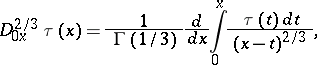and 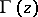is the Euler gamma-function.

The solution of the problem (1), (3) reduces in turn to finding the function 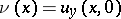from some singular integral equation. This equation in the case when 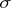is the curve

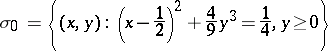has the form

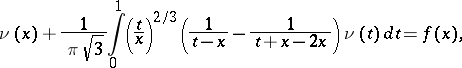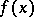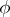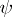where is expressed explicitly in terms of and , and the integral is understood in the sense of the Cauchy principal value (see [1]–[4]).

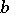
In the proof of the uniqueness and existence of the solution of the Tricomi problem, in addition to the Bitsadze extremum principle (see Mixed-type differential equation) and the method of integral equations, the so-called method is used, the essence of which is to construct for a given second-order differential operator 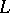(for example, 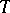) with domain of definition 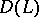, a first-order differential operator

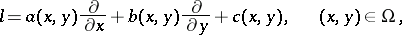with the property that

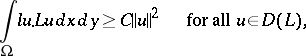where 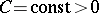and is a certain norm (see [5]).

The Tricomi problem has been generalized both to the case of mixed-type differential equations with curves of parabolic degeneracy (see [6]) and to the case of equations of mixed hyperbolic-parabolic type (see [7]).

References

[1]	F. Tricomi, "On second-order linear partial differential equations of mixed type" , Moscow-Leningrad (1947) (In Russian; translated from Italian)
[2]	F.G. Tricomi, "Equazioni a derivate parziale" , Cremonese (1957)
[3]	A.V. Bitsadze, "Zum Problem der Gleichungen vom gemischten Typus" , Deutsch. Verlag Wissenschaft. (1957) (Translated from Russian)
[4]	A.V. Bitsadse, "Equations of mixed type" , Pergamon (1964) (Translated from Russian)
[5]	L. Bers, "Mathematical aspects of subsonic and transonic gas dynamics" , Wiley (1958)
[6]	A.M. Nakhushev, "A boundary value problem for an equation of mixed type with two lines of degeneracy" Soviet Math. Dokl. , 7 : 5 (1966) pp. 1142–1145 Dokl. Akad. Nauk SSSR , 170 (1966) pp. 38–40
[7]	T.D. Dzhuraev, "Boundary value problems for equations of mixed and mixed-composite type" , Tashkent (1979) (In Russian)

Comments

Using a functional-analytic method, S. Agmon [a5] has investigated more general equations. Fourier integral operators were used by R.J.P. Groothuizen [a2].

For additional references see also Mixed-type differential equation.

References

[a1]	P.R. Garabedian, "Partial differential equations" , Wiley (1964)
[a2]	R.J.P. Groothhuizen, "Mixed elliptic-hyperbolic partial differential operators: a case-study in Fourier integral operators" , CWI Tracts , 16 , CWI , Amsterdam (1985) (Thesis Free University Amsterdam)
[a3]	M.M. Smirnov, "Equations of mixed type" , Amer. Math. Soc. (1978) (Translated from Russian)
[a4]	T.V. Gramtcheff, "An application of Airy functions to the Tricomi problem" Math. Nachr. , 102 (1981) pp. 169–181
[a5]	S. Agmon, "Boundary value problems for equations of mixed type" G. Sansone (ed.) , Convegno Internaz. Equazioni Lineari alle Derivati Parziali (Trieste, 1954) , Cremonese (1955) pp. 65–68