Thom isomorphism

An isomorphism between the (generalized) (co)homology groups of the base space of a vector (sphere) bundle and the (co)homology groups of its Thom space .

Suppose the -dimensional vector bundle over a finite cell complex is oriented in some multiplicative generalized cohomology theory (cf. Generalized cohomology theories), that is, there exists a Thom class . Then is an -module, and the homomorphism , given by multiplication by the Thom class, is an isomorphism, called the Thom isomorphism (or Thom–Dold isomorphism).

There is a dually-defined isomorphism .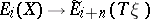

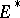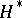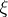In the case where is the classical cohomology theory , the isomorphism is described in [1], and it was established for an arbitrary theory in [2]. Moreover, if is not oriented in the integral cohomology theory , then there is an isomorphism 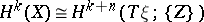, where the right-hand side is the cohomology group with coefficients in the local system of groups . More generally, if is non-oriented in the cohomology theory , there is an isomorphism which generalizes both the Thom isomorphism described above and the Thom–Dold isomorphism for 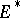-oriented bundles [3].

References

[1]	R. Thom, "Quelques propriétés globales des variétés différentiables" Comm. Math. Helv. , 28 (1954) pp. 17–86
[2]	A. Dold, "Relations between ordinary and extraordinary homology" , Colloq. Algebraic Topology, August 1–10, 1962 , Inst. Math. Aarhus Univ. (1962) pp. 2–9
[3]	Yu.B. Rudyak, "On the Thom–Dold isomorphism for nonorientable bundles" Soviet Math. Dokl. , 22 (1980) pp. 842–844 Dokl. Akad. Nauk. SSSR , 255 : 6 (1980) pp. 1323–1325
[4]	R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975)