Thinness of a set
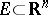 at a point
at a point 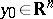
A local criterion for the fact that 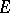 is a polar set. A non-empty set
is a polar set. A non-empty set 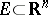 is said to be thin at the point
is said to be thin at the point 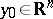 in two cases:
in two cases:
1) 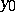 is not a limit point of
is not a limit point of 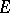 ; that is,
; that is, 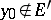 , where
, where 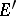 is the derived set of
is the derived set of 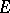 ;
;
2) 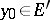 and there exists a superharmonic function
and there exists a superharmonic function 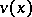 in a neighbourhood of
in a neighbourhood of 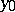 (see Superharmonic function) such that
(see Superharmonic function) such that
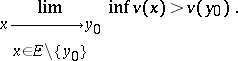 |
The set 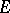 is polar if and only if it is thin at each of its points. For an arbitrary set
is polar if and only if it is thin at each of its points. For an arbitrary set 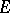 the subset of those points at which
the subset of those points at which 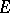 is thin is polar. Any non-empty subset of a set which is thin at the point
is thin is polar. Any non-empty subset of a set which is thin at the point 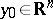 is thin at
is thin at 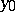 . The union of a finite number of sets thin at the point
. The union of a finite number of sets thin at the point 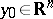 is a set thin at
is a set thin at 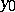 .
.
A segment in the plane 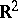 is not a thin set at any of its points. If
is not a thin set at any of its points. If 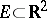 is a thin set at a point
is a thin set at a point 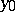 , then there exist arbitrarily small discs with centre
, then there exist arbitrarily small discs with centre 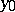 and not intersecting
and not intersecting 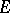 . A polar set
. A polar set 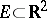 is completely discontinuous. However, the Cantor set on the
is completely discontinuous. However, the Cantor set on the  -axis (which is of measure zero) is not thin at any of its points. At the same time, for example, in
-axis (which is of measure zero) is not thin at any of its points. At the same time, for example, in 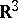 the set of points
the set of points
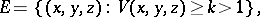 |
which has a spine at the point 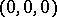 , where
, where
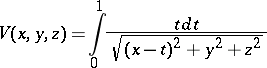 |
is the Newton potential with density 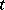 on the segment
on the segment 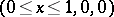 , is a thin set at the spine
, is a thin set at the spine 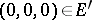 (Lebesgue's example).
(Lebesgue's example).
References
| [1] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1969) |
| [2] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
Comments
Two further interesting properties of thinness are: 1) 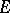 is thin at
is thin at  if and only if
if and only if  is not a limit point of
is not a limit point of 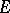 with respect to the fine topology; and 2) a boundary point
with respect to the fine topology; and 2) a boundary point  of an open set
of an open set 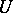 , bounded if
, bounded if 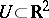 , is regular for the Dirichlet problem if and only if the complement of
, is regular for the Dirichlet problem if and only if the complement of 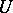 is not thin at
is not thin at  .
.
The concept of thinness, and its use to define a fine topology, is fundamental in any potential theory. For example, in probabilistic potential theory associated to a strong Markov process, a Borel set 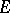 is thin at
is thin at  if and only if, starting from
if and only if, starting from  , the process almost surely will not hit
, the process almost surely will not hit 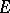 even once. But, in general, a set thin at each of its points is not polar; a countable union of such sets is called a semi-polar set, a kind of exceptional set (related to the Dirichlet problem) which can be considerably bigger than a polar set when the potential theory lacks symmetry (for example, for the heat equation potential theory). Roughly speaking, a set
even once. But, in general, a set thin at each of its points is not polar; a countable union of such sets is called a semi-polar set, a kind of exceptional set (related to the Dirichlet problem) which can be considerably bigger than a polar set when the potential theory lacks symmetry (for example, for the heat equation potential theory). Roughly speaking, a set 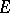 is polar (respectively semi-polar) in probabilistic potential theory if the process almost surely never meets
is polar (respectively semi-polar) in probabilistic potential theory if the process almost surely never meets 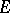 (respectively, only meets
(respectively, only meets 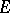 at most a countable number of times). See also Potential theory, abstract.
at most a countable number of times). See also Potential theory, abstract.
References
| [a1] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
Thinness of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thinness_of_a_set&oldid=48966