Suzuki group
A simple finite group 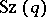 , a member of the infinite series of simple groups, discovered by M. Suzuki.
, a member of the infinite series of simple groups, discovered by M. Suzuki.
Let  be a natural number, let
be a natural number, let 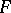 be the finite field with
be the finite field with 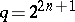 elements, and let
elements, and let 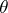 be an automorphism of
be an automorphism of 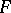 such that
such that 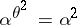 for any
for any 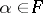 . The Suzuki group
. The Suzuki group 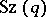 is then generated by the subgroup
is then generated by the subgroup 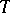 consisting of all diagonal matrices of order 4 with diagonal elements
consisting of all diagonal matrices of order 4 with diagonal elements 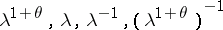 (
(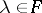 ,
, 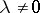 ), the subgroup
), the subgroup 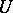 consisting of all triangular matrices of the form
consisting of all triangular matrices of the form
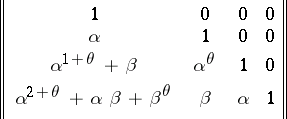 |
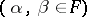 , and the matrix
, and the matrix
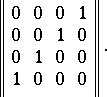 |
The subgroup 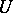 is a Sylow
is a Sylow  -subgroup of the group
-subgroup of the group 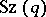 ; it is a Suzuki
; it is a Suzuki  -group. The subgroup
-group. The subgroup  coincides with the normalizer of the subgroup
coincides with the normalizer of the subgroup 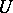 . The permutation representation of the group
. The permutation representation of the group 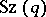 on the cosets of
on the cosets of 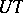 is doubly transitive; its degree is equal to
is doubly transitive; its degree is equal to 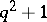 . The order of the Suzuki group
. The order of the Suzuki group 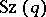 is equal to
is equal to 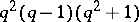 , and is not divisible by 3. On the other hand, any non-Abelian finite simple group whose order is not divisible by 3 is isomorphic to a Suzuki group. The group
, and is not divisible by 3. On the other hand, any non-Abelian finite simple group whose order is not divisible by 3 is isomorphic to a Suzuki group. The group 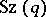 is a maximal subgroup of the symplectic group
is a maximal subgroup of the symplectic group 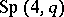 and is the centralizer in
and is the centralizer in 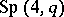 of an automorphism of order 2 of the group
of an automorphism of order 2 of the group 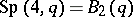 . In other words,
. In other words, 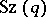 is isomorphic to
is isomorphic to 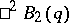 — the twisted analogue of a Chevalley group of type
— the twisted analogue of a Chevalley group of type 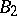 over the field with
over the field with 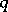 elements.
elements.
References
| [1] | M. Suzuki, "On a class of doubly transitive groups" Ann. of Math. , 75 : 1 (1962) pp. 105–145 |
| [2] | R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972) |
Comments
There is in fact precisely one automorphism 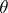 of
of 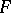 such that
such that 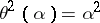 for all
for all 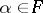 . It is
. It is 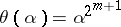 .
.
There is a twisted polarity whose absolute points are the 
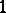 -dimensional subspaces of
-dimensional subspaces of 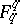 that are fixed by a conjugate of
that are fixed by a conjugate of  . The set of absolute points thus obtained is an ovoid. See [a1]–[a2].
. The set of absolute points thus obtained is an ovoid. See [a1]–[a2].
References
| [a1] | J. Tits, "Ovoïdes et groupes de Suzuki" Arch. Math. , 13 (1962) pp. 187–198 |
| [a2] | J. Tits, "Une propriété charactéristique des ovoïdes associés aux groupes de Suzuki" Arch. Math. , 17 (1966) pp. 136–153 |
| [a3] | B. Huppert, "Finite groups" , 3 , Springer (1982) pp. Chapt. IX.3 |
Suzuki group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Suzuki_group&oldid=48916