Spherical functions

solid spherical harmonics, associated Legendre functions of the first and second kinds

Two linearly independent solutions and of the differential equation

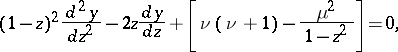where and are complex constants, which arises in the solution of a class of partial differential equations by the method of separation of variables (cf. Separation of variables, method of). The points are branching points of the solutions, in general. The spherical functions are particular cases of the hypergeometric functions (cf. Hypergeometric function):

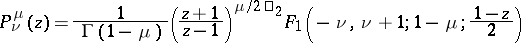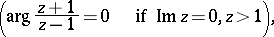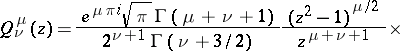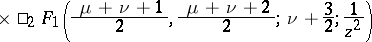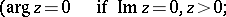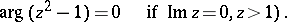The spherical functions 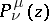and 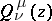are defined and single-valued in the domains 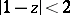and 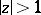, respectively, of the complex plane cut by the real axis from 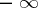to .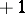

If , , , 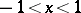then the following functions are usually taken as solutions:

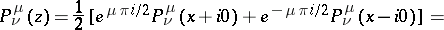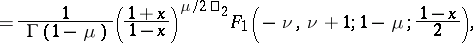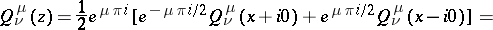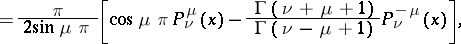where 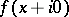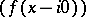are the values of the function on the upper (lower) boundary of the cut.

When , are the Legendre polynomials. For zonal spherical functions see Spherical harmonics.

References

[1]	H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953)
[2]	E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)
[3]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6
[4]	A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960)
[5]	E.W. Hobson, "The theory of spherical and ellipsoidal harmonics" , Chelsea, reprint (1955)

Comments

A more common usage of the phrase "spherical function" is as follows.

Let 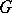be a unimodular locally compact group and 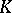a subgroup of 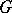. Let 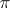be an irreducible unitary representation of 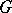on a Hilbert space such that the 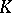-fixed vectors in form a one-dimensional subspace, spanned by a unit vector . Then the 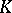-bi-invariant functi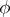on on 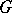defined by 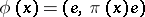is called a spherical function. Sometimes is called a zonal spherical function, while the functions (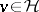) are also called spherical functions. Some authors call 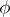an elementary spherical function, while all 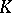-bi-invariant functions on 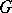are called spherical functions.

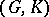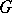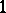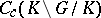The pair is a Gel'fand pair if, for all irreducible unitary representations of , the subspace of -fixed vectors in the representation space has dimension or . This is equivalent to the commutativity of the convolution algebra of 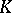-bi-invariant continuous functions on 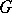with compact support. Now spherical functions are more generally defined as solutions 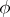, not identically zero, of the functional equation

(*)

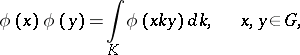where 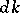is the normalized Haar measure on . These solutions include the spherical functions associated with irreducible unitary representations. Other solutions may be associated with irreducible non-unitary representations of . The characters of the comutative algebra 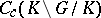are precisely the mappings 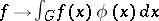, where 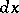is Haar measure on 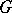and is a solution of (*).

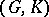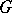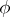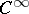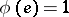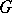If is, moreover, a connected Lie group, then is a Gel'fand pair if and only if the algebra of -invariant differential operators on the homogeneous space is commutative. Then is a solution of (*) if and only if it is -bi-invariant, , , and the function on is a joint eigenfunction of the elements of . In particular, if is a connected real semi-simple LIe group and 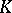is a maximal compact subgroup, then is a Gel'fand pair, 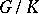is a Riemannian symmetric space, and much information is available about 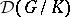and the sperical functions.

References

[a1]	J. Fauraut, "Analyse harmonique sur les paires de Gelfand et les espaces hyperboliques" , Anal. Harmonique , CIMPA (1982) pp. 315–446
[a2]	I.M. Gel'fand, "Spherical functions on symmetric spaces" Transl. Amer. Math. Soc. , 37 (1964) pp. 39–44 Dokl. Akad. Nauk SSSR , 70 (1950) pp. 5–8
[a3]	R. Godement, "Introduction aux traveaux de A. Selberg" Sem. Bourbaki , 144 (1957)
[a4]	S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4