Smoothness, modulus of
The modulus of continuity of the derivative of order  of a function
of a function  defined on a Banach space
defined on a Banach space  , i.e. the expression
, i.e. the expression
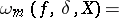 |
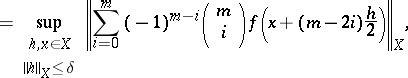 |
where  . If
. If  , the modulus of smoothness is the ordinary modulus of continuity (cf. Continuity, modulus of) of
, the modulus of smoothness is the ordinary modulus of continuity (cf. Continuity, modulus of) of  . Basic properties of the modulus of smoothness (in the case
. Basic properties of the modulus of smoothness (in the case  and the space of continuous functions) are:
and the space of continuous functions) are:
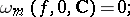 |
 does not decrease together with
does not decrease together with 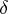 ;
;
if 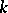
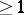 is an integer, then
is an integer, then
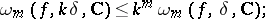 |
for any 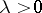 ,
,
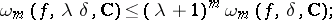 |
if 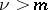 , then
, then
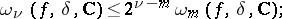 |
if 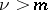 , then
, then
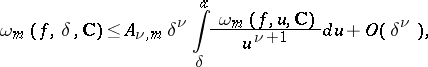 |
where  and
and  are constants independent of
are constants independent of  .
.
Certain problems in the theory of approximation of functions can ultimately be solved only in terms of a modulus of smoothness of order 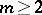 . In the theory of approximations of functions an important class is the class of periodic continuous functions with period
. In the theory of approximations of functions an important class is the class of periodic continuous functions with period  and with second-order modulus of smoothness satisfying the condition
and with second-order modulus of smoothness satisfying the condition
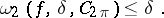 |
The modulus of continuity of such functions satisfies the condition
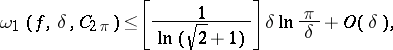 |
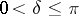 , and the constant
, and the constant 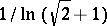 cannot be improved [4].
cannot be improved [4].
References
| [1] | S.N. Bernshtein, "Sur l'ordre de la meilleure approximation des fonctions continués par de polynomes de degré donné" Mem. Publ. Classe Sci. Acad. Belgique (2) , 4 (1912) pp. 1–103 |
| [2] | A. Marchaud, "Sur les dérivées et sur les différences des fonctions de variables réelles" J. Math. Pures Appl. , 6 (1927) pp. 337–425 |
| [3] | A. Zygmund, "Smooth functions" Duke Math. J. , 12 (1945) pp. 47–76 |
| [4] | A.V. Efimov, "Estimate of the modules of continuity of a function in the class 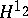 " Izv. Akad. Nauk SSSR Ser Mat. , 21 (1957) pp. 283–288 (In Russian) " Izv. Akad. Nauk SSSR Ser Mat. , 21 (1957) pp. 283–288 (In Russian) |
Comments
The modulus of smoothness 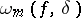 is also written in terms of symmetric differences, as
is also written in terms of symmetric differences, as  , where
, where
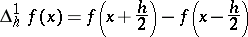 |
and
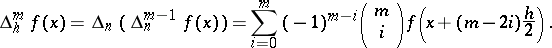 |
This gives a recurrent procedure for computing (approximations of) it.
To overcome certain shortcomings of this (classical) modulus of smoothness (especially its ability to characterize the order of the best polynomial approximation 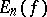 to a function
to a function 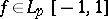 ), new moduli of smoothness have been introduced. They use so-called step-weight functions
), new moduli of smoothness have been introduced. They use so-called step-weight functions 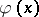 , and are defined by
, and are defined by
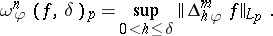 |
The function  is chosen for the problem at hand. Note that here the increment
is chosen for the problem at hand. Note that here the increment 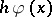 varies with
varies with  . A basic result is that
. A basic result is that 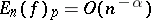 if and only if
if and only if 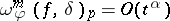 . (Here
. (Here  ,
, 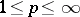 ,
,  ,
,  , and approximation is in
, and approximation is in 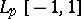 .) For more on such moduli, their use in
.) For more on such moduli, their use in  approximation problems and in the interpolation of spaces, see [a1].
approximation problems and in the interpolation of spaces, see [a1].
References
| [a1] | Z. Ditzian, V. Totik, "Moduli of smoothness" , Springer (1987) |
| [a2] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) |
Smoothness, modulus of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smoothness,_modulus_of&oldid=48741