Small image
From Encyclopedia of Mathematics
of a set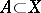 
under a mapping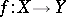 
The set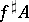 
of all 
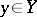for which 
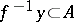. An equivalent definition is: 
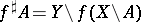. Closed and irreducible mappings may be characterized by means of small images. A continuous mapping 
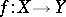is closed (cf. Closed mapping) if and only if the small image 
of each open set 
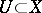is open. A continuous mapping 
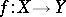onto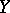 
is closed and irreducible (cf. Irreducible mapping) if and only if the small image of each non-empty open set 
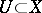is a non-empty set.
How to Cite This Entry:
Small image. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Small_image&oldid=48735
Small image. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Small_image&oldid=48735
This article was adapted from an original article by V.V. Fedorchuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article