Serre subcategory
A locally small full subcategory 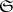 of an Abelian category
of an Abelian category  such that for every exact sequence
such that for every exact sequence
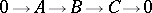 |
in  it is the case that
it is the case that  if and only if
if and only if  and
and  . In this context, local smallness of a category is the condition: A collection of representatives of the isomorphism classes of subobjects of any object forms a set. Serre subcategories can be characterized as kernels of functors defined on
. In this context, local smallness of a category is the condition: A collection of representatives of the isomorphism classes of subobjects of any object forms a set. Serre subcategories can be characterized as kernels of functors defined on  .
.
Given a Serre subcategory, one can define the quotient category  , whose objects are the objects of
, whose objects are the objects of  and whose morphisms are defined by
and whose morphisms are defined by
 |
The quotient category 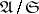 is Abelian.
is Abelian.
A Serre subcategory is called localizing if the canonical functor  has a right adjoint
has a right adjoint 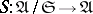 , called the section functor. If
, called the section functor. If 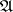 is a Grothendieck category with coproducts, then a Serre subcategory is localizing if and only if it is closed under coproducts. Thus one obtains a generalization of the classical theory of localization of modules over a commutative ring. This method embraces many constructions of rings of fractions and torsion theories (radicals) of modules over associative rings.
is a Grothendieck category with coproducts, then a Serre subcategory is localizing if and only if it is closed under coproducts. Thus one obtains a generalization of the classical theory of localization of modules over a commutative ring. This method embraces many constructions of rings of fractions and torsion theories (radicals) of modules over associative rings.
The concept of a Serre subcategory was introduced by J.-P. Serre [1], who called them classes. By using this concept he obtained a far-reaching generalization of a theorem of Hurewicz (see Homotopy group).
References
| [1] | J.-.P. Serre, "Groupes d'homotopie et classes de groupes abéliens" Ann. of Math. , 58 : 2 (1953) pp. 258–294 |
| [2] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
| [3] | N. Popesco, P. Gabriel, "Caractérisations des catégories abéliennes avec générateurs et limites inductives exactes" C.R. Acad. Sci. Paris , 258 : 17 (1964) pp. 4188–4190 |
Comments
Serre subcategories are also called thick subcategories or dense subcategories. See also Localization in categories.
References
| [a1] | N. Popescu, "Abelian categories with applications to rings and modules" , Acad. Press (1973) |
Serre subcategory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Serre_subcategory&oldid=48679